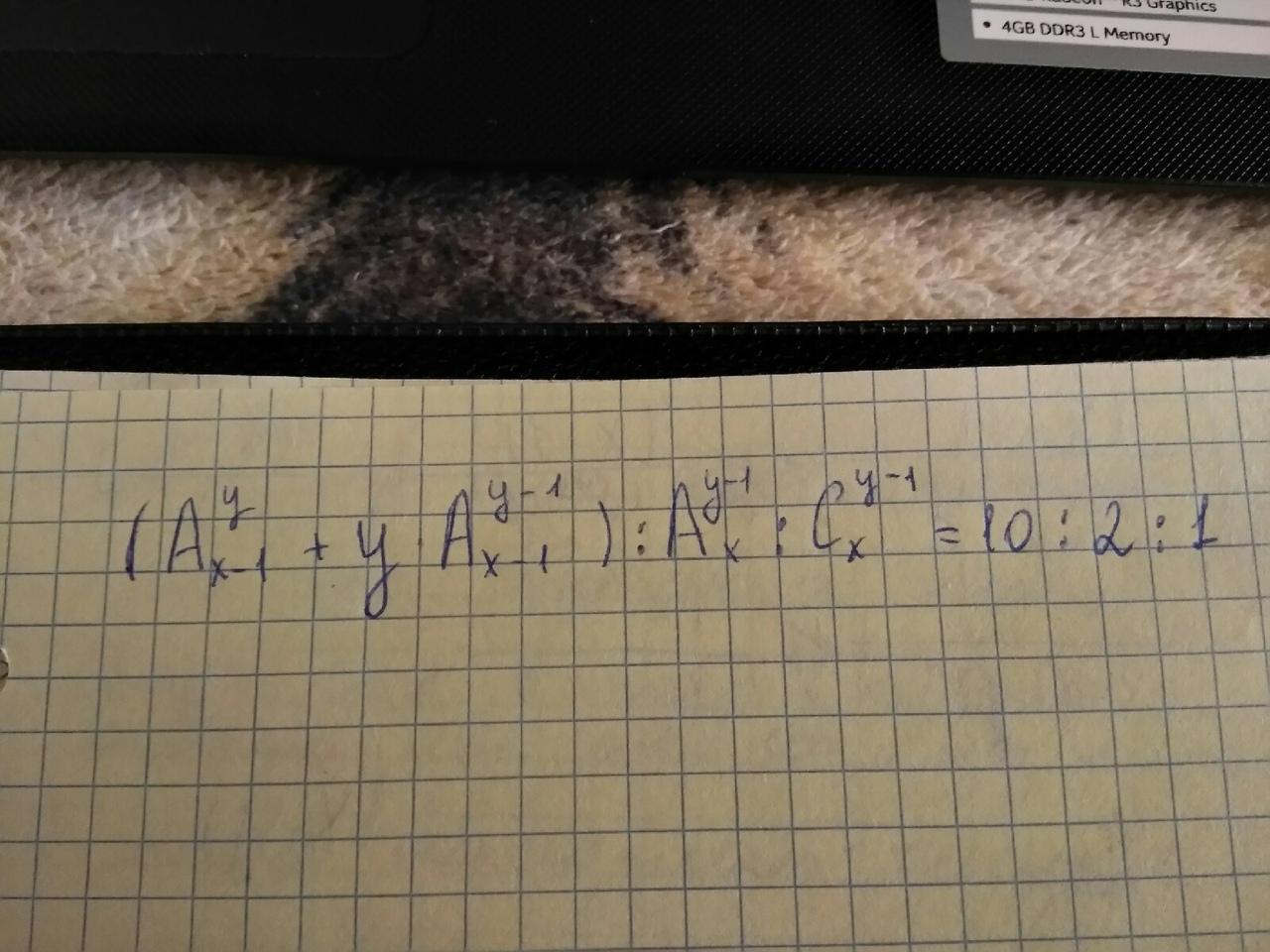Question

Помогите пожалуйста с решением комбинаторного уравнения! Много баллов даю!

Answer 1

Ответ:

x = 7, y =3.

Пошаговое объяснение:

Из формул для числа размещений и сочетаний следует, что $A^{y-1}_x = C_x^{y-1} cdot (y-1)!$.

По условию, $A_x^{y-1} = 2 cdot C_x^{y-1}$. Отсюда $(y-1)! = 2$ и $y = 3$. Будем считать, что $x - 1 geq y$, то есть, $x geq 4$.

Поскольку $A^3_{x-1} = (x-1) cdot (x-2) cdot (x-3), A^2_{x-1} = (x-1) cdot (x-2), A_x^2 = x(x-1)$,

то получаем уравнение

$(x-1)cdot (x-2) cdot (x-3) + 3 cdot (x-1) cdot (x-2) = frac{10}{2} cdot x cdot (x-1)$

Поскольку $x geq 4$, то мы можем разделить обе части уравнения на $x - 1$

$(x-2) cdot (x-3) + 3 cdot (x-2) = 5 cdot x\(x-2) cdot x = 5 cdot x \ x = 7$

Проверка:

$C_7^2 = frac{7 cdot 6}{2} = 21, A_7^2 = 7 cdot 6 = 42 = 2 cdot 21, \\A_6^3 + 3 cdot A_6^2 = 6 cdot 5 cdot 4 + 3 cdot 6 cdot 5 = 6 cdot 5 cdot 7 = 210 = 10 cdot 21.$