Question

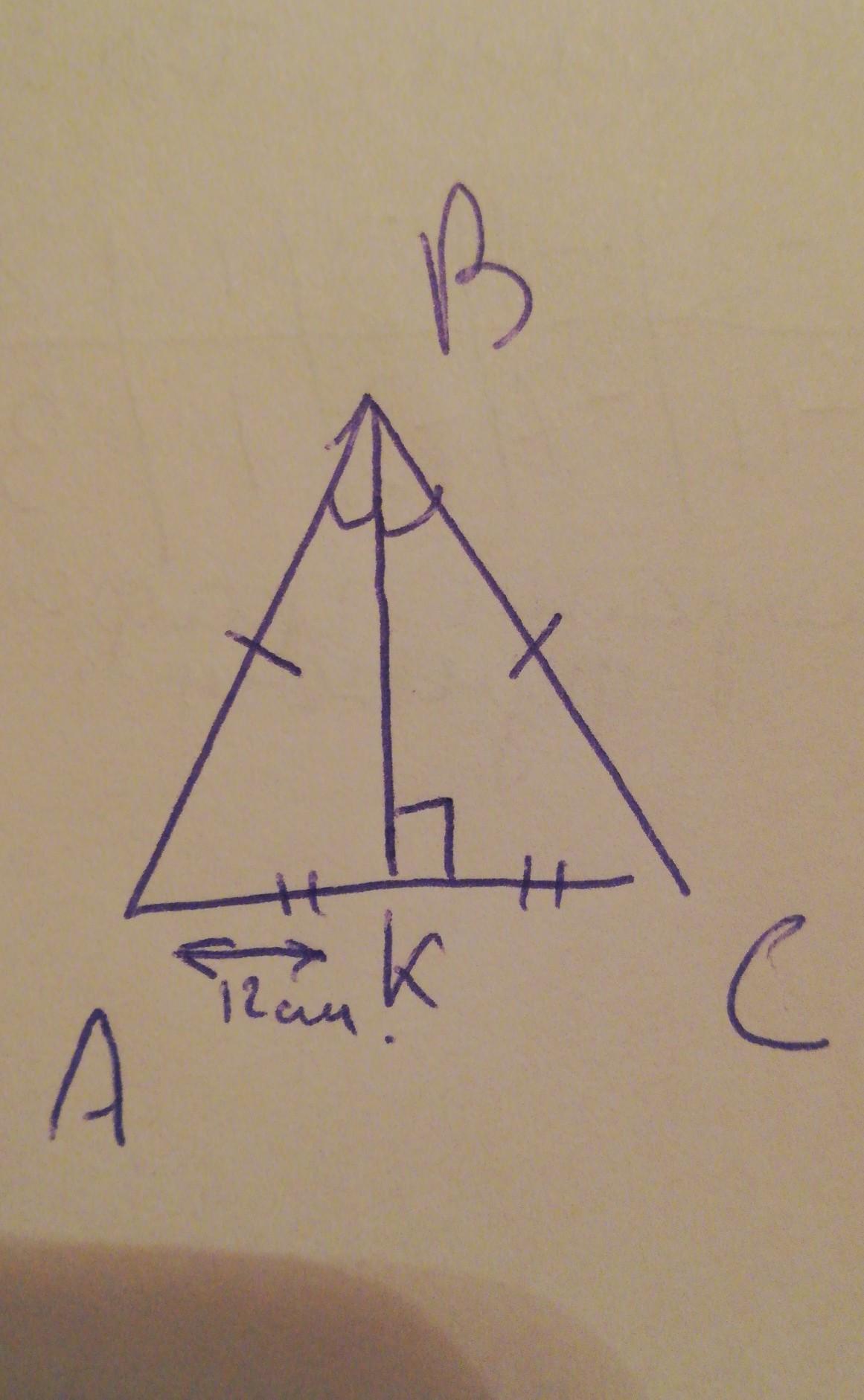
В треугольнике ABC стороны AB и BC равны, BK - биссектриса. AK равен 12 см.
Найдите длину AC и угол AKB
Прошу помогите,даю 35 баллов!

Answer 1

Ответ :

AC=24 см

АКВ=90°

Answer 2

Или как?)

Answer 3

ну или так

Answer 4

кидай

Answer 5

1 мин

Answer 6

id362606214

Answer 7

1. Так как ВК - биссектриса, то по ее свойству АК/КС=АВ/ВС=1, т.к. АК=ВК, значит, АС=АК+КС=12+12=24/см/.

2. ΔАВС равнобедренный ПО ОПРЕДЕЛЕНИЮ  РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА. Значит, ∠ВАС=∠ВСА, пусть эти углы равны α, тогда ∠АВС =180°-2α, но т.к. ВК - биссектриса, то ∠АВК=(180°-2α)=90°-α.

3. В ΔАВК   ∠АКВ= 180°-∠КАВ-∠АВК=180°-α-( 90°-α)=180°-α-90°+α=90°

Ответ. АС=24см

           Угол АКВ = 90градусов.

Удачи!