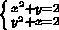Ответы
Ответ дал:
0
Из первого уравнения выразим у:
Подставим во второе уравнение:
При
При
Ответ: {- 2; - 2}; {1; 1}; {}; {
}
Ответ дал:
0
СПАСИБО ВАМ!!!
Ответ дал:
0
Удачи Вам!
Ответ дал:
0
OK
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад