Question

найдите объем куба, известна диагональ основания 8м

Answer 1

Ответ:

$V=(4sqrt{2})^{3} =128sqrt{2}$

Пошаговое объяснение:

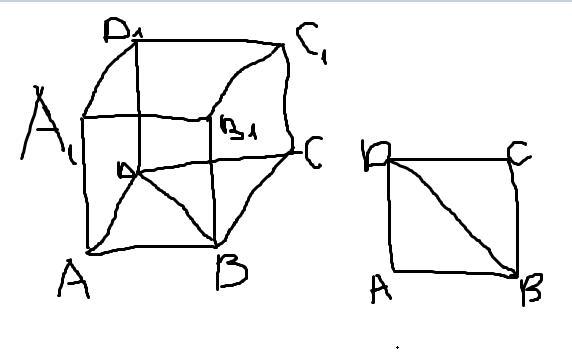
объем куба равен его стороне в кубе :$V=a^{3}$

Зная диагональ, мы можем найти стороны.

Рассмотрим треугольник ABD. Он прямоугольный (угол А= 90 градусов, т.к. по условию у нас куб). Так же из того, что у нас куб вытекает следующее: AB=AD=x

Мы знаем диагональ и две стороны, которые приняли за х

т.к. треугольник прямоугольный, мы можем применить теорему Пифагора

$x^{2} +x^{2}  = 8^{2} \\2x^{2} =64\\x^{2} = 32\x=4sqrt{2}$

или $x=-4sqrt{2}$

но корень с минусом нам не подходить, так как длина стороны не может быть отрицательной

следовательно сторона куба равна $4sqrt{2}$

$V=(4sqrt{2})^{3} =128sqrt{2}$