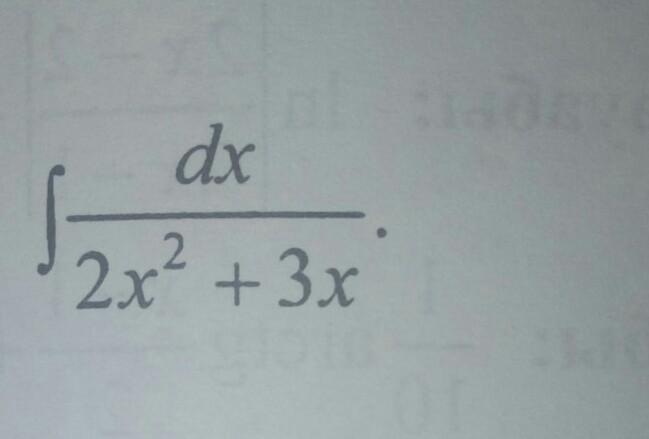Question

Нужно найти неопределенный интеграл.​

Answer 1

$int frac{dx}{2x^2+3x}=int frac{dx}{x(2x+3)}=int Big (frac{1}{3x}-frac{2}{3(2x+3)}Big )dx=frac{1}{3}ln|x|-frac{2}{3cdot 2}ln|2x+3|+C=\\=frac{1}{3}cdot (ln|x|-ln|2x+3|)+C=frac{1}{3}cdot lnBig |frac{x}{2x+3}Big |+C; ;\\\frac{1}{x(2x+3)}=frac{A}{x}+frac{B}{2x+3}=frac{A(2x+3)+Bx}{x(2x+3)}\\A(2x+3)+Bx=1\\x=0:; ; A=frac{1}{2x+3}=frac{1}{3}\\x=-frac{3}{2}:; ; B=frac{1}{x}=-frac{2}{3}\\frac{1}{x(2x+3)}=frac{1}{3x}-frac{2}{3(2x+3)}$

Answer 2

Ответ неправильный. Правильный ответ: 1:3ln×модуль х:х+3:2 модуль +С.

Answer 3

вообще-то у него во второй строке правильный ответ; то, что написано в последних строках, - это промежуточные действия во время нахождения коэффициентов при раскладывании правильной рациональной дроби...

Answer 4

Ответ верный....Просто сам ответ можно преобразовывать до того вида, который записан в ответе.

Answer 5

А вы можете преобразать?

Answer 6

Ещё можно 1/3 внести под знак ln , будет =ln sqrt[3]{|x/2x+3|}+C