Question

Помогите пожалуйста, дам 35 баллов.

Answer 1

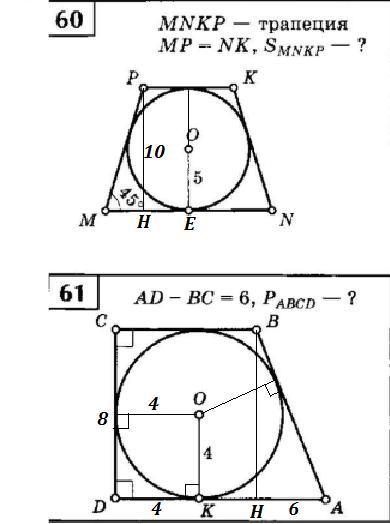
Задание 60.

Формула площадь равнобедренной трапеции если в нее вписана окружность:

$S=frac{4R^{2} }{sinalpha} =frac{4R^{2} }{sinbeta }=frac{4*5^{2} }{sin45} =frac{100}{frac{sqrt{2} }{2}}=frac{200}{sqrt{2}} =100sqrt{2}$

Answer 2

60)  MNKP - равнобедренная трапеция. МР=KN , R(вписан)=OE=5,  ∠PMN=∠KNM=α=45° .

Так как окружность вписанная, то должно выполняться условие: MP+NK=MN+PK (сумма боковых сторон = сумме оснований).

Тогда средняя линия трапеции  $m=frac{MN+PK}{2}=frac{MP+NK}{2}$  .

Высота трапеции РН⊥MN , обозначим h=PH=2R=10.

Рассм. ΔМРH: ∠РНМ=90° , ∠РМН=45°  ⇒  ∠МРН=90°-45°=45°  ⇒  ΔМРН - равнобедренный  ⇒  РН=МН=10,  МР=h/sinα (α=45°) , MP=10/(√2/2)=10√2 .

$S=frac{MN+PK}{2}cdot PH=frac{MP+NK}{2}cdot 10=frac{2MP}{2}cdot 10=MPcdot 10=\\=10sqrt2cdot 10=100sqrt2$

Или:

$S=frac{MN+PK}{2}cdot PH=frac{MP+NK}{2}cdot h=frac{2MP}{2}cdot h=MPcdot h=frac{h}{sinalpha }cdot h=\\=frac{h^2}{sinalpha }=frac{(2R)^2}{sinalpha }=frac{4R^2}{sinalpha }=frac{4cdot 25}{sin45^circ }=frac{100}{sqrt2/2}=100sqrt2$

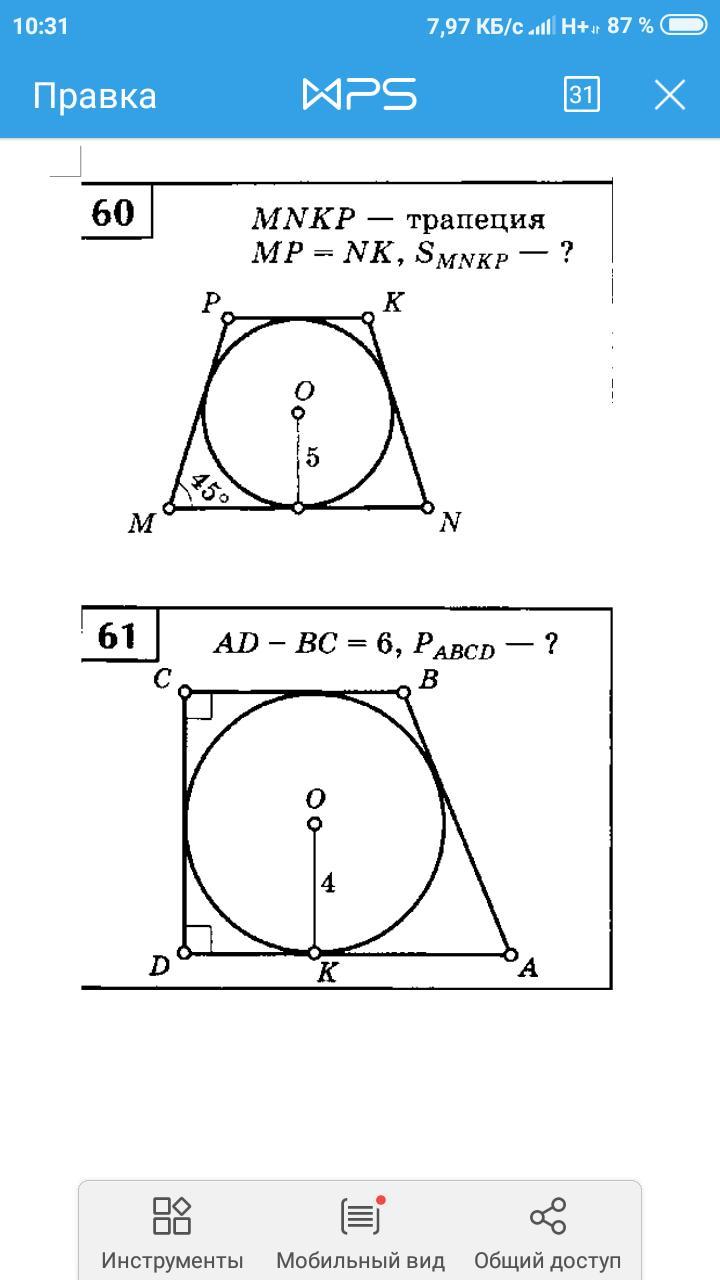
61)  ABCD - трапеция , ∠D=∠C=90° , R(вписан)=OK=4 .

Высота трапеции ВН=2R=CD=8 , AD-BC=AD-DH=AH , AH=6 ,

ΔABH: по теореме Пифагора АВ=√(8²+6²)=√100=10.

Cумма оснований трапеции = сумме её боковых сторон, т.к. в трапецию вписана окружность, тогда СD+АВ=AD+CB=8+10=18 .

Р(ABCD)=CD+CB+AB+AD=18+18=2*18=36 .