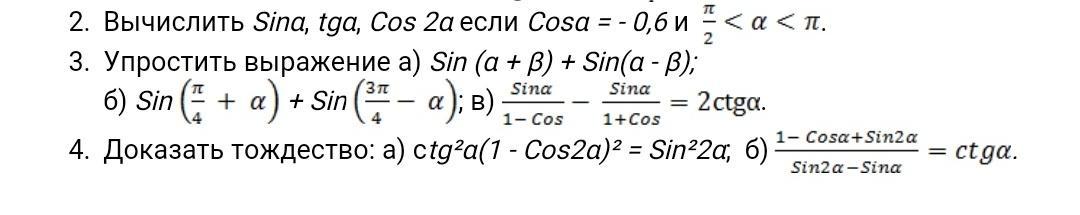Question

ОООЧЕНЬ СРОЧНО!!!!
ХОТЬ КАКОЕ-НИБУДЬ ЗАДАНИЕ!!!

Answer 1

2) α - угол второй четверти значит Sinα > 0 , tgα < 0

$Sinalpha=sqrt{1-Cos^{2}alpha} =sqrt{1-(-0,6)^{2} }=sqrt{1-0,36}=sqrt{0,64}=0,8\\tgalpha=frac{Sinalpha }{Cosalpha }=frac{0,8}{-0,6}=-1frac{1}{3}\\Cos2alpha =2Cos^{2}alpha-1=2*(-0,6)^{2}-1=0,72-1=-0,28$

3а) Sin(α + β) + Sin(α - β) = SinαCosβ + CosαSinβ + SinαCosβ - CosαSinβ =

= 2SinαCosβ

3б)

$Sin(frac{pi }{4}+alpha)+Sin(frac{3pi }{4}-alpha)=2Sinfrac{frac{pi }{4}+alpha+frac{3pi }{4}-alpha}{2}Cosfrac{frac{pi }{4}+alpha-frac{3pi }{4}+alpha}{2}=2Sinfrac{pi }{2}Cos(alpha-frac{pi }{4})=2Cos(alpha-frac{pi }{4})$

3в)

$frac{Sinalpha }{1-Cosalpha }-frac{Sinalpha }{1+Cosalpha }=frac{Sinalpha+Sinalpha Cosalpha-Sinalpha+Sinalpha Cosalpha}{(1-Cosalpha)(1+Cosalpha)}=frac{2Sinalpha Cosalpha}{1-Cos^{2}alpha}=frac{2Sinalpha Cosalpha}{Sin^{2}alpha}=frac{2Cosalpha }{Sinalpha }=2Ctgalpha\\2Ctgalpha=2Ctgalpha$

Тождество доказано

4а)

$Ctg^{2} alpha(1-Cos2alpha)^{2}=frac{Cos^{2}alpha} {Sin^{2}alpha}*(2Sin^{2}alpha)^{2} =4Cos^{2}alpha Sin^{2}alpha=Sin^{2}2alpha$