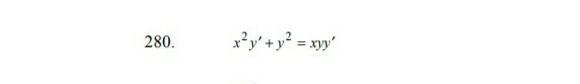Ответы
Ответ дал:
0
Преобразуем данное уравнение:

Последнее уравнение есть однородное уравнение. Решим его методом замены переменной.
Пусть

тогда

—уравнение с разделяющимися переменными

—общее решение исходного уравнения
Последнее уравнение есть однородное уравнение. Решим его методом замены переменной.
Пусть
тогда
—уравнение с разделяющимися переменными
—общее решение исходного уравнения
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад