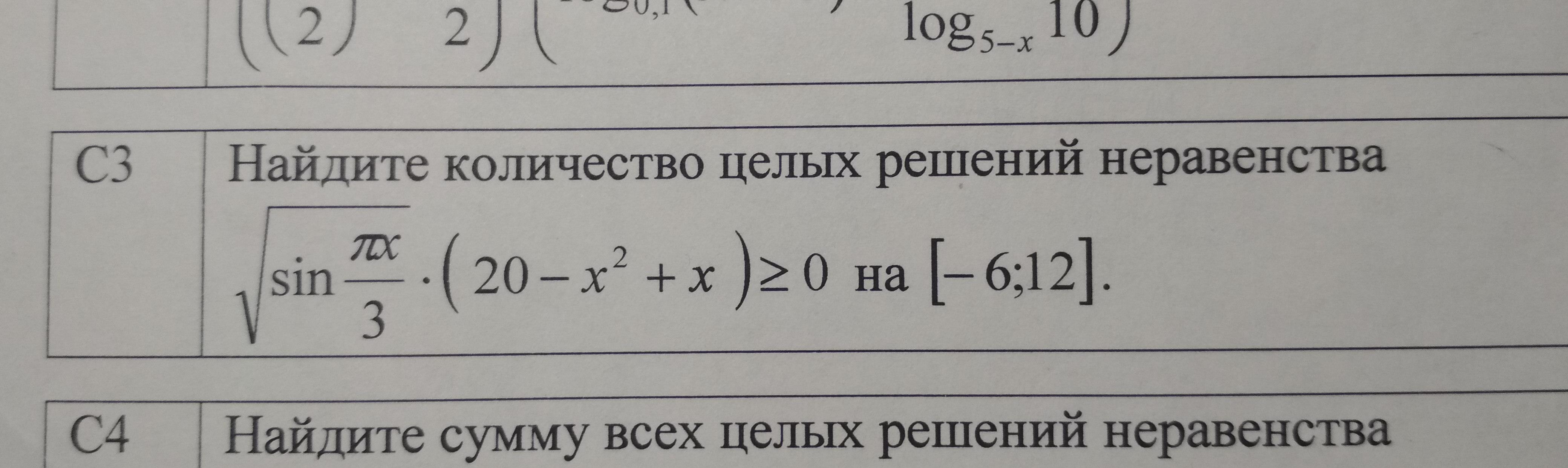Question

Найдите количество целых решений неравенства:

Answer 1

$sqrt{sindfrac{pi x}{3}}cdot(20-x^2+x)geq0$

Рассмотрим ограничение, накладываемое квадратным корнем.

$sindfrac{pi x}{3}geq0 Leftrightarrow 2pi kleqdfrac{pi x}{3}leq pi+2pi k Leftrightarrow 6kleq xleq 6k+3, k in mathbb{Z}$

Областью допустимых значений неравенства на промежутке [-6; 12] будет x∈[-6; -3]∪[0; 3]∪[6; 9]∪{12}.

Вернемся к неравенству. Так как корень квадратный является числом неотрицательным при любых значениях x, можно выполнить следующий равносильный переход.

$sqrt{sindfrac{pi x}{3}}cdot(20-x^2+x)geq0 Leftrightarrow left [ begin{array}{I} 20-x^2+x geq 0 \ sin dfrac{pi x}{3}=0 end{array} Leftrightarrow left [ begin{array}{I} xin[-4; 5] \ x=3k, k in mathbb{Z} end{array}$

С учетом ОДЗ на промежутке получим решения x∈{-6}∪[-4; -3]∪[0; 3]∪{6}∪{9}∪{12}. Таким образом, при заданном условии неравенство имеет 10 целых решений.

Ответ: 10

Answer 2

Огромное спасибо!