Question

помогите пжжжддд дам 10 баллов​

Answer 1

По-видимому, надо найти длины сторон треугольника.

Треугольник равнобедренный. Следовательно, высота, опущенная извершины, является и биссектрисой угла М. Т.е. угол М 60°

Два угла В и С в равнобедренном треугольнике равны, обозначим их через х.

х+х+60=180° (сумма всех углов треугольника)

2х=180-60=120°

х=60°

Треугольник равносторонний. ВМ=МС=ВС

Рассмотрим треугольник ВАМ. Он прямоугольный, угол В=60°, угол М=30° АМ=6см

cos30°=√3/2

Следовательно гипотенуза ВМ=6 ÷ √3/2≈6,92

Ответ ВМ=МС=ВС≈6,92 см

Answer 2

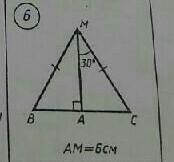
Дано: ΔBMC, BM = MC, AM - высота, ∠AMC = 30°, AM = 6 см.

Найти: AB - ?

Решение:

Рассмотрим ΔAMC

cosM = cos30° = √3/2

Косинус угла прямоугольного треугольника - отношение прилежащего катета к гипотенузе

$displaystylett cosM=frac{AM}{MC}\\\frac{sqrt{3}}{2}=frac{6}{MC}\\12=MCsqrt{3}\\\MC=frac{12}{sqrt{3}}=frac{12sqrt{3} }{sqrt{3}cdotsqrt{3}}=4sqrt{3}$

По теореме Пифагора

$displaystylett AC=sqrt{MC^2-AM^2}\\AC=sqrt{(4sqrt{3})^2-6^2}\\AC=sqrt{48-36}=sqrt{12}=2sqrt{3}~cm$

Рассмотрим ΔBMC

BM = MC ==> ΔBMC - равнобедренный

AM - высота

Высота прямоугольного треугольника, проведенная к основанию, есть медиана, т. е. делит основание на 2 равные части

==> AC = AB = 2√3 см

Ответ: AB = 2√3 см