1. Дан куб
ABCDA1B1C1D1 , длина ребра которого равна a. На ребре AA1 взята точка E
так, что AE a/4. Найти объём пирамиды, вершиной которой является точка
A1, а основанием – сечение куба, проходящее через точки D и E, и произвольную внутреннюю точку ребра BB1.
Ответы
Ответ дал:
0
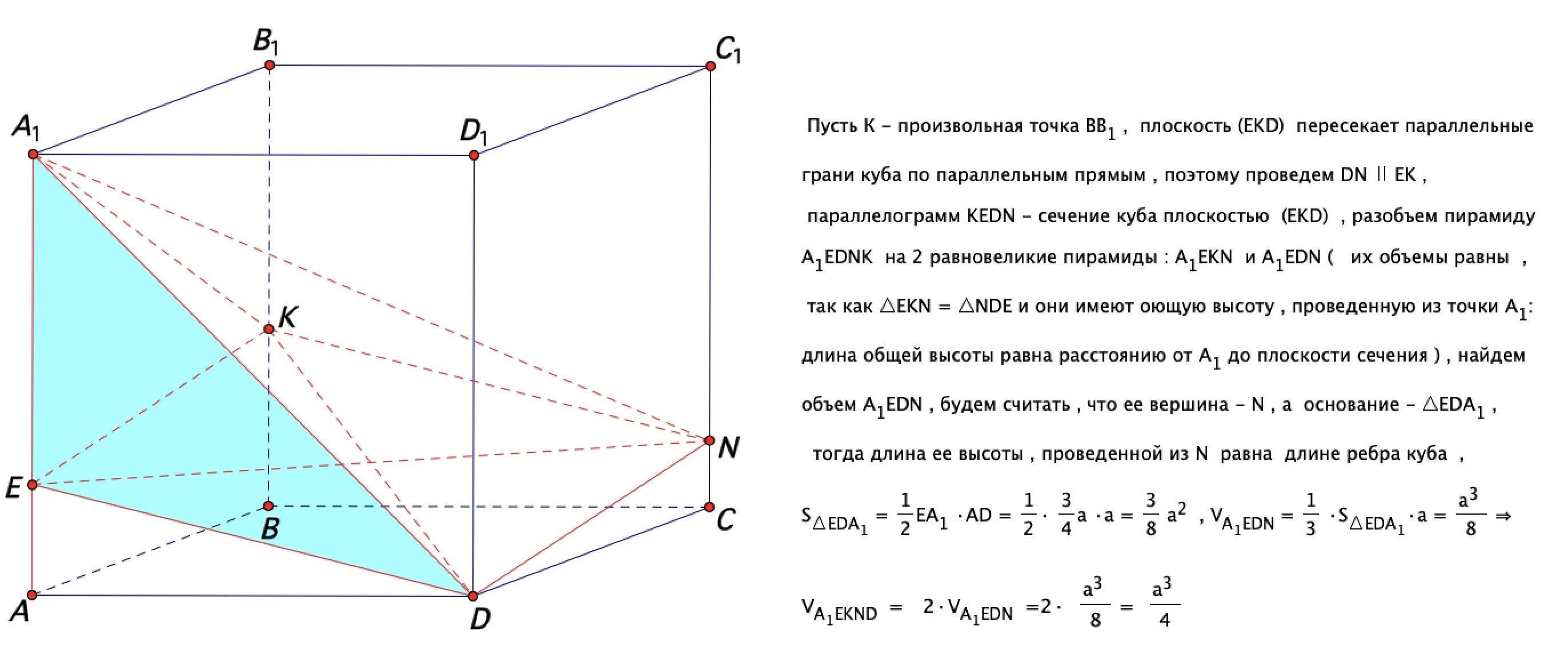
Решение : /////////////////////////////////
Приложения:
Ответ дал:
0
Почему высота, проведенная из точки N, равна ребру куба?
Ответ дал:
0
прямая СС1 параллельна DD1 и значит параллельна плоскости ADD1 , а тогда расстояние от точки N до этой грани равно расстоянию от точки С до этой грани , то есть ребру куба
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад