AB и AC - радиусы, угол ВАС = 90. Найдите площадь закрашенной части.
Помогите, пожалуйста
Приложения:
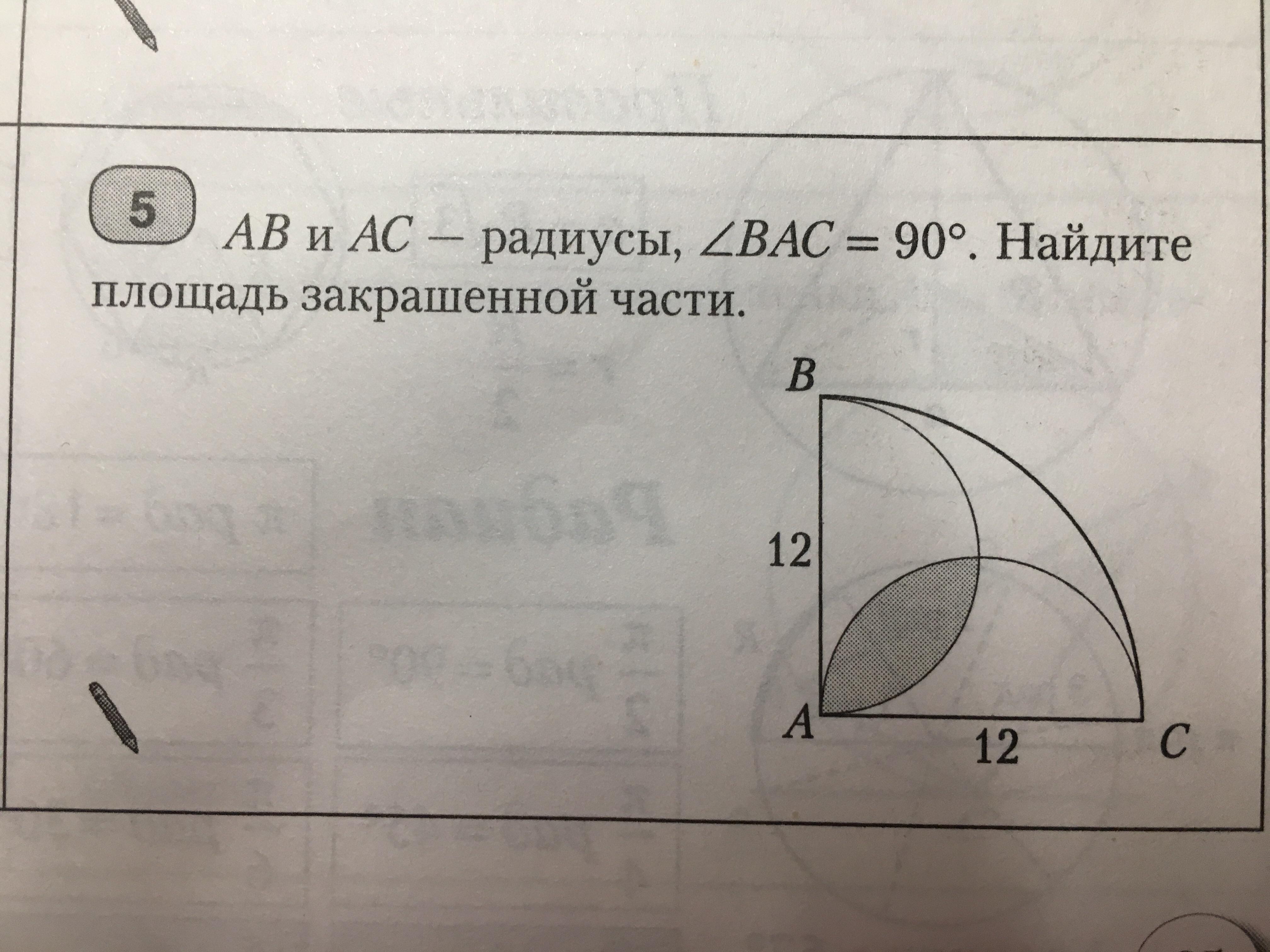
Ответы
Ответ дал:
0
Полуокружности пересекаются в точке D.
ADB=ADC=90 (опираются на диаметры), BDC - развернутый угол. В прямоугольном равнобедренном треугольнике BAC:
ABD=ACD=45, дуги искомой фигуры 90.
Искомая площадь составлена из двух сегментов, ф=90, r=6.
Sсегм= пr^2 *ф/360 - r^2*sinф /2
S= 2*36(п/4 -1/2) = 18(п-2) ~20,55
Ответ дал:
0
Но ведь это только один сегмент
Ответ дал:
0
Четверть окружности с радиусом 6 =9п. Треугольник с катетами 6 =18. Сегмент равен их разности =9(п-2). Два сегмента = 18(п-2).
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад