Question

из точки не лежащей в плоскости, приведены перпендикуляр и наклонная угол между которыми 60°
найти длины и перпендикуляр и проекций, если длина наклонной равна 8 см.​

Answer 1

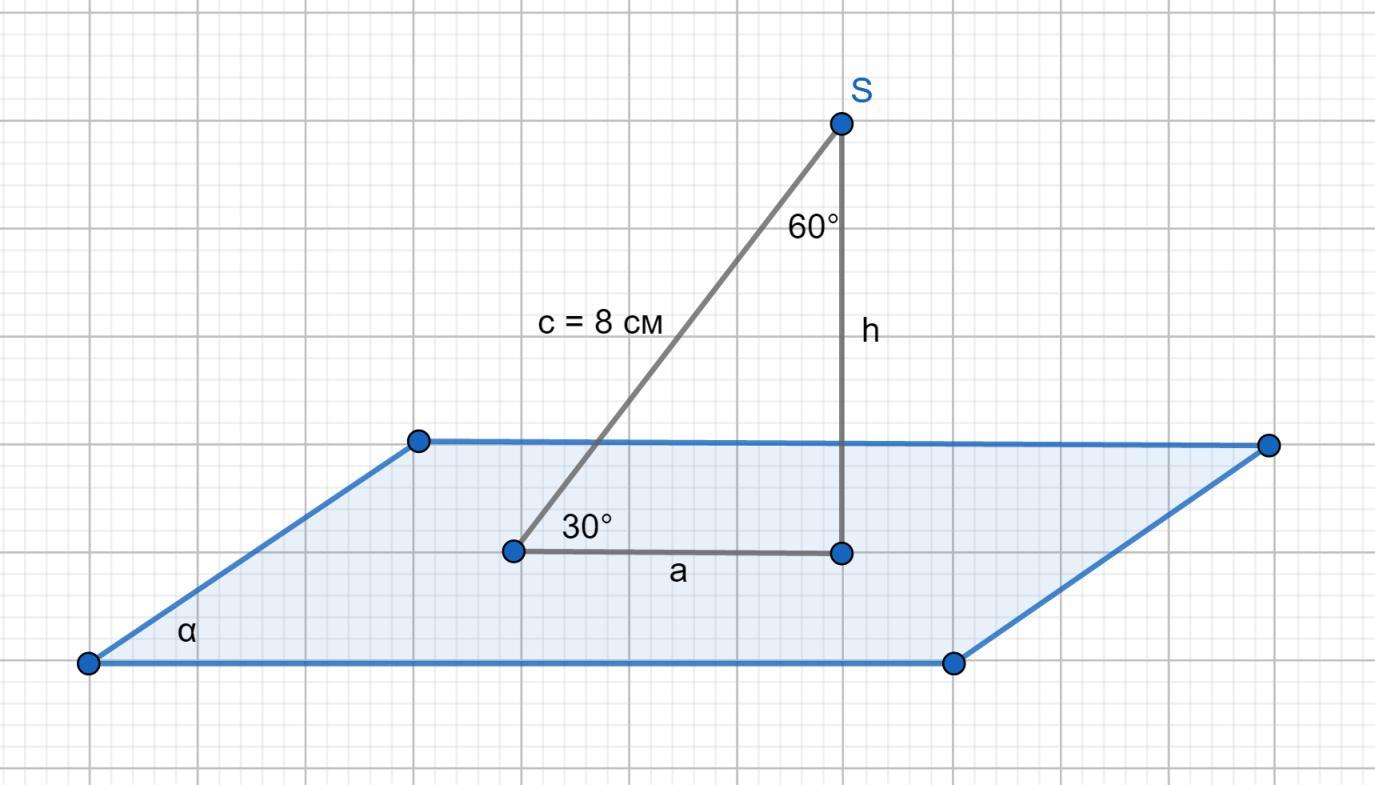
В полученном прямоугольном треугольнике угол между наклонной c и ее проекцией a составляет 30° (180° - 90° - 60° = 30°).

Катет, лежащий против угла 30°, равен половине гипотенузы. ⇒ h = 4 см.

Проекцию a найдем по т. Пифагора.

a = √(8² - 4²) = √(64 - 16) = √48 = √16*3 = 4√3

перпендикуляр = 4 см, проекция наклонной = 4√3 см.