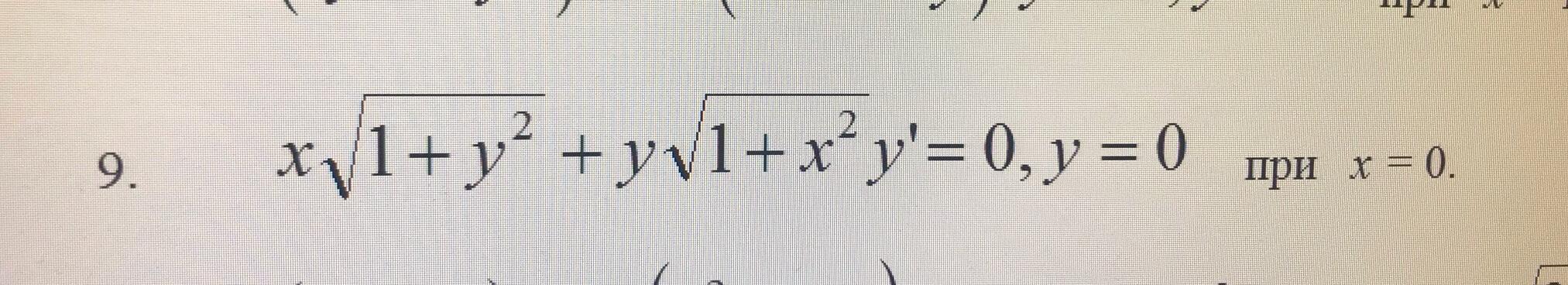Question

Буду очень благодарна

Answer 1

$x sqrt{1 + {y}^{2} } + y sqrt{1 + {x}^{2} } {y}^{ prime} = 0$
—уравнение с разделяющимися переменными
$x sqrt{1 + {y}^{2} } + y sqrt{1 + {x}^{2} } frac{dy}{dx} = 0 \ x sqrt{1 + {y}^{2} } dx + y sqrt{1 + {x}^{2} } dy = 0 \ frac{x}{ sqrt{1 + {x}^{2} } } dx + frac{y}{ sqrt{1 + {y}^{2} } } dy = 0 \ intfrac{x}{ sqrt{1 + {x}^{2} } } dx + intfrac{y}{ sqrt{1 + {y}^{2} } } dy = 0 \ intfrac{2x}{ 2sqrt{1 + {x}^{2} } } dx + intfrac{2y}{2 sqrt{1 + {y}^{2} } } dy = 0 \ int frac{d(1 + {x}^{2}) }{2 sqrt{1 + {x}^{2} } } + int frac{d(1 + {y}^{2}) }{2 sqrt{1 + {y}^{2} } } = 0 \ sqrt{1 + {x}^{2} } + sqrt{1 + {y}^{2} } = c$
— общее решение.
Найдем частное решение, используя начальное условие у(0)=0 .
$sqrt{1 + {0}^{2} } + sqrt{1 + {0}^{2} } =c \ 1 + 1 = c \ c = 2$
Таким образом,
$sqrt{1 + {x}^{2} } + sqrt{1 + {y}^{2} } = 2$
—частное решение.