Question

Задание на тему пирамида. Объясните пожалуйста)

Answer 1

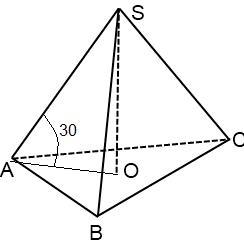
Рассмотрим прямоугольный ΔAOS

AO=R=AB/V3=30/V3=10V3

tg<SAO=SO/AO

SO=AO*tg30=10V3/V3=10

Answer 2

а вот AO найти можно

Answer 3

это радиус описанной окружности

Answer 4

не согласен?

Answer 5

AO=AB/V3=30/V3=10V3

Answer 6

Нет, я полностью согласен. Это правильно

Answer 7

Т.к. пирамида правильная. то высота проектируется в  центр основания - равностороннего треугольника. Высоту основания можно найти как а√3/2, где а=30, высота равна 30√3/2=15√3.

проекцией бокового ребра будет 2/3 от высоты основания, т.е. радиус описанной около прав. треуг. окружности. Эта проекция равна 2*15√3/3=10√3

А высота пирамиды может быть найдена, как произведение проекции бок. ребра на тангенс 30°.

10√3*√3/3=10/дм/

Ответ 10 дм.

ДОп... здесь надо обосновать контрольный момент - угол между прямой и плоскостью = это угол между прямой и проекцией прямой на плоскость. Это к слову про угол наклона бок. ребра к плоск. основания.