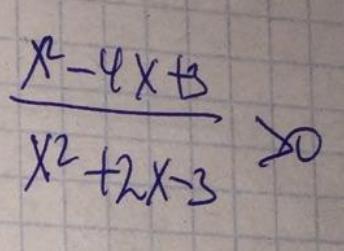Ответы
Ответ дал:
0
.........................
Приложения:
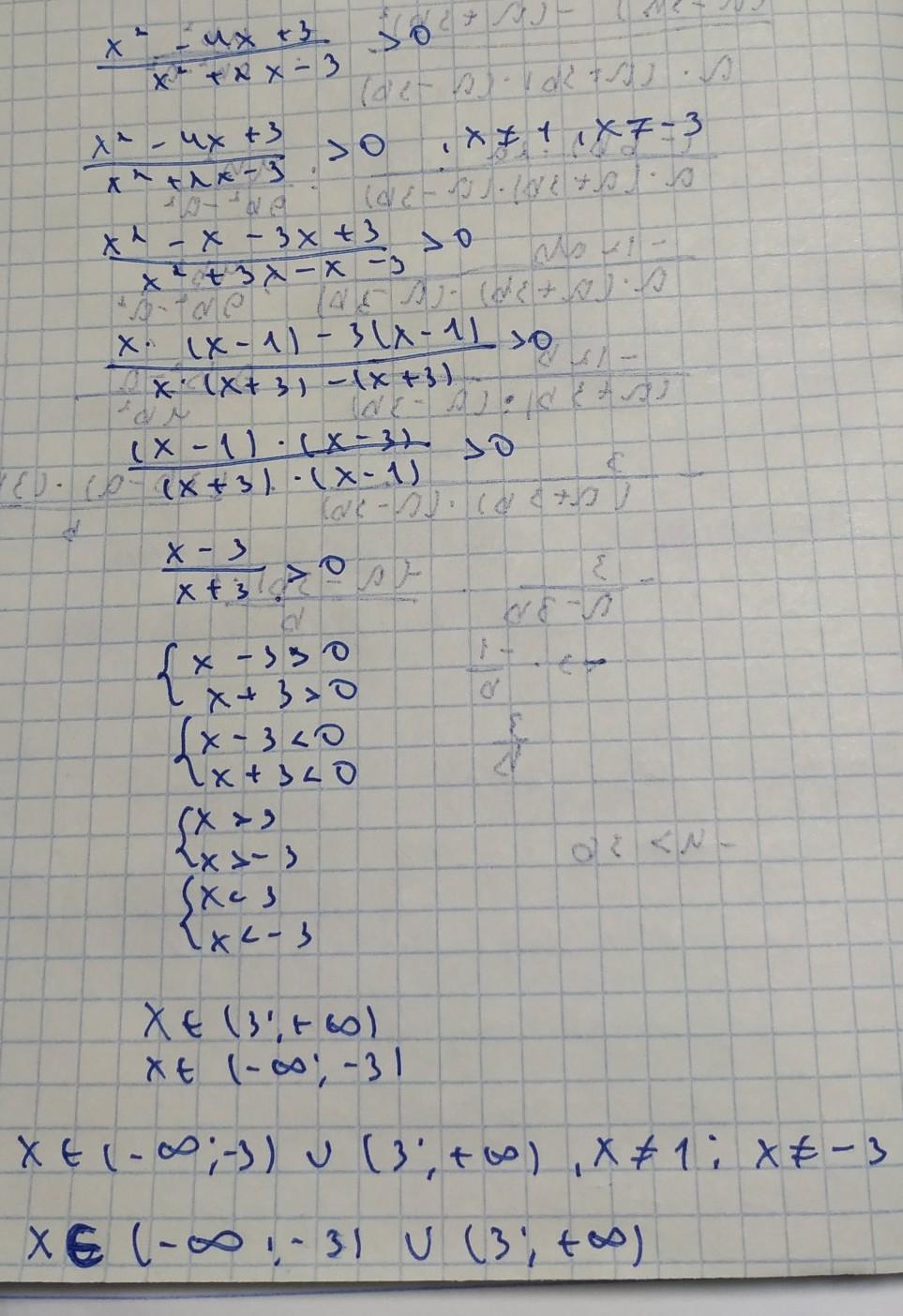
Ответ дал:
0
Разложим на множители выражения из числителя и знаменателя.
Таким образом
Уберём одинаковые корни
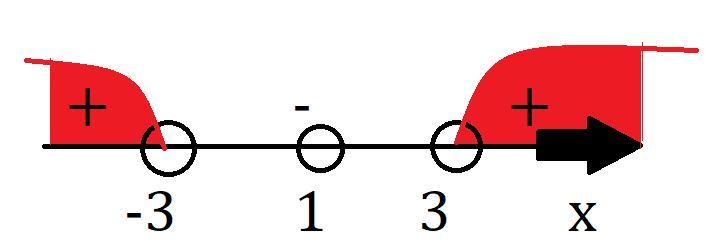
Используем метод интервалов, чтобы найти значения удовлетворяющие неравенству, см. ниже, я сразу же отметил ещё, что х≠1.
Ответ: x∈(-∞;-3)∪(3;+∞)
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад