Вычислить предел в примере В), НЕ пользуясь правилом Лопиталя. Если можно решите подробно.
Приложения:
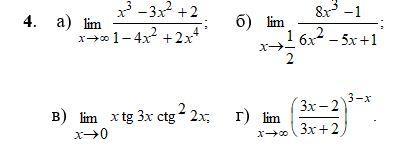
Ответы
Ответ дал:
0
Ответ: 3/4.
Пошаговое объяснение:
1. Так как при x⇒0 бесконечно малые величины tg(3*x) и 3*x эквивалентны, то при вычислении предела можно заменить tg(3*x) на 3*x.
2. Так как ctg(2*x)=1/tg(2*x), то ctg²(2*x)=1/tg²(2*x). А так как при x⇒0 бесконечно малые величины tg(2*x) и 2*x эквивалентны, то при вычислении предела можно заменить tg(2*x) на 2*x, а следовательно, 1/tg²(2*x) - на 1/(2*x)²=1/(4*x²).
Тогда lim(x⇒0) x*tg(3*x)*ctg²(2*x)=lim(x⇒0) x*3*x*1/(4*x²)=lim(x⇒0) (3*x²)/(4*x²)=3/4.
Ответ дал:
0
Вы написали: "Так как ctg(2*x)=1/tg(2*x)", а разве не ctg(x)= cos(x)/sin(x)?
Ответ дал:
0
"lim(x⇒0) (3*x²)/(4*x²)=3/4" в ответе остается 3/4 иксы сокращаются?
Ответ дал:
0
Вам разве неизвестно тригонометрическое тождество tg(x)*ctg(x)=1? А что изменится, если в нём заменить x на 2*x?
Ответ дал:
0
А если у вас возникают сомнения в вопросе с сокращением "иксов", то вам явно рано изучать пределы.
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
9 лет назад