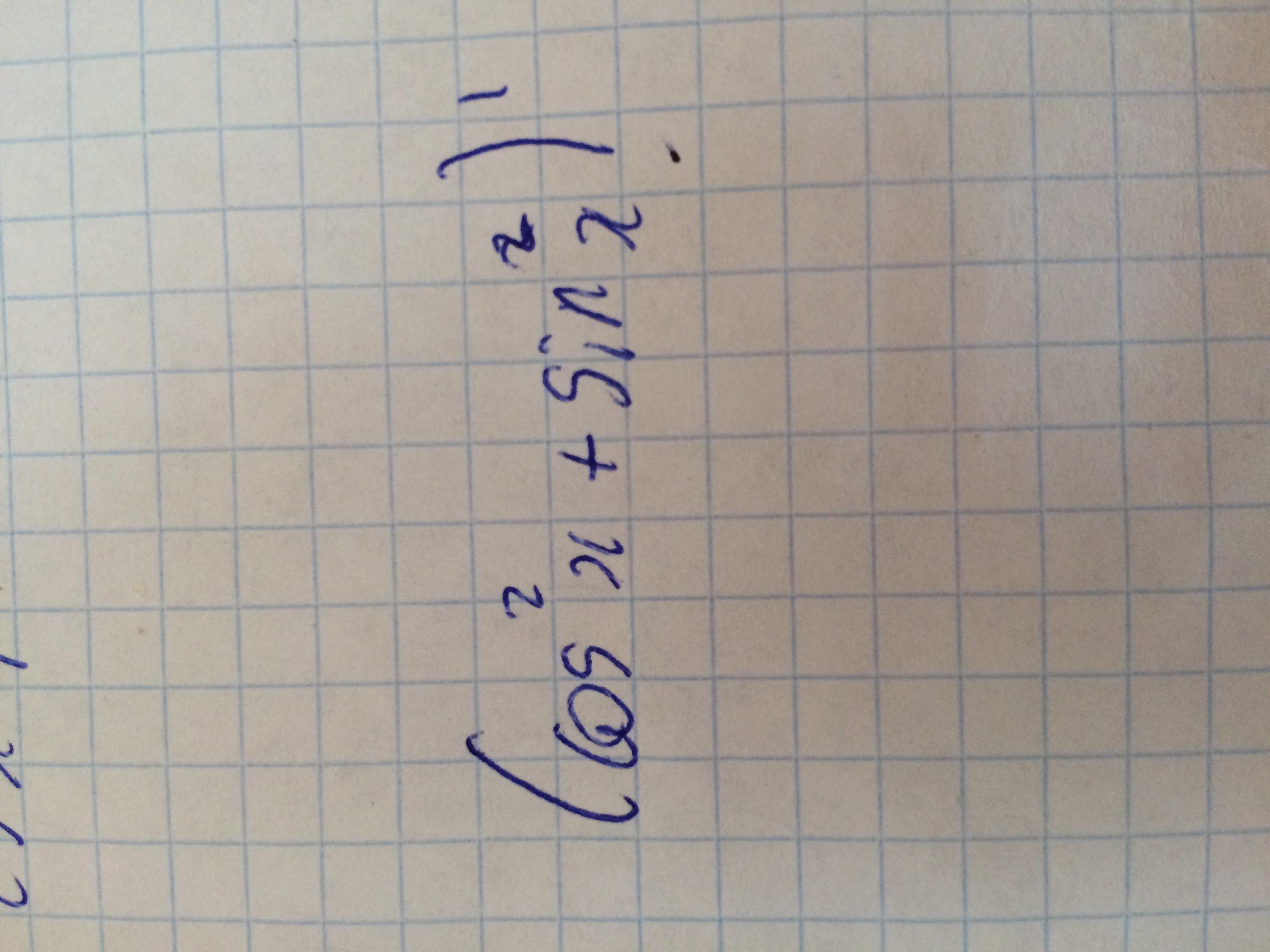Question

Очень срочно нужно

Алгебра 10 класс

Answer 1

g(x),f(x)-какие-то функции от аргумента х.

$(g(x)+f(x))'=g'(x)+f'(x)\f(g(x))'=f'(g(x))*g'(x)\(x^n)'=n*x^{n-1}\cos'{x}=-sin{x}\sin'{x}=cos{x}$

$(cos^2{x}+sin^2{x})'\(1)'=0$

По основному тригонометрическому тождеству выражение в скобках равняется 1, а производна от константы это 0. Ну или:

$(cos^2{x}+sin^2{x})'=(cos^2{x})'+(sin^2{x})'=\2cos^{2-1}{x}*(cos{x})'+2sin^{2-1}{x}*(sin{x})'=\-2cos{x}*sin{x}+2sin{x}*cos{x}=0$