Question

Помогите решить задачу по теме "Окружности". Ответ, который должен получиться при правильном решении записан в конце.
Заранее спасибо :)

Answer 1

Ответ:

8

Объяснение:

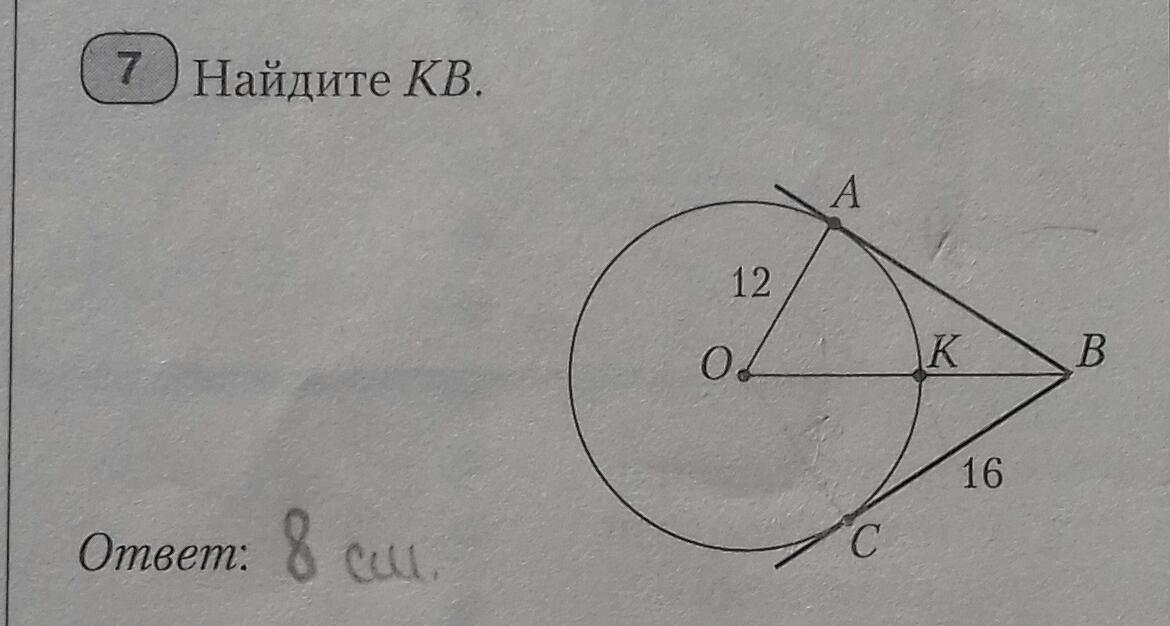
AB=CD=16, касательные проведённый из одной точки к окружности.

по т. Пифогора для Δ OAB

OA²+AB²=OB²

12²+16²=400

OB=√400=20

KB = OB-OK

OK = 12 - радиус

KB=20-12= 8

Answer 2

Отрезки касательных ВА и ВС  по свойству отрезков касательных, проведенных к окружности  из точки В,  равны. ОА ⊥ АВ, тоже по свойству радиуса, проведенному в точку касания. Поэтому

ОВ=√(16²+12²)=√(256+144)=20

ОК=ОА= 12, как радиусы одной окружности. Поэтому искомый отрезок КВ= ОВ-ОК=20-12=8

Ответ 8