Question

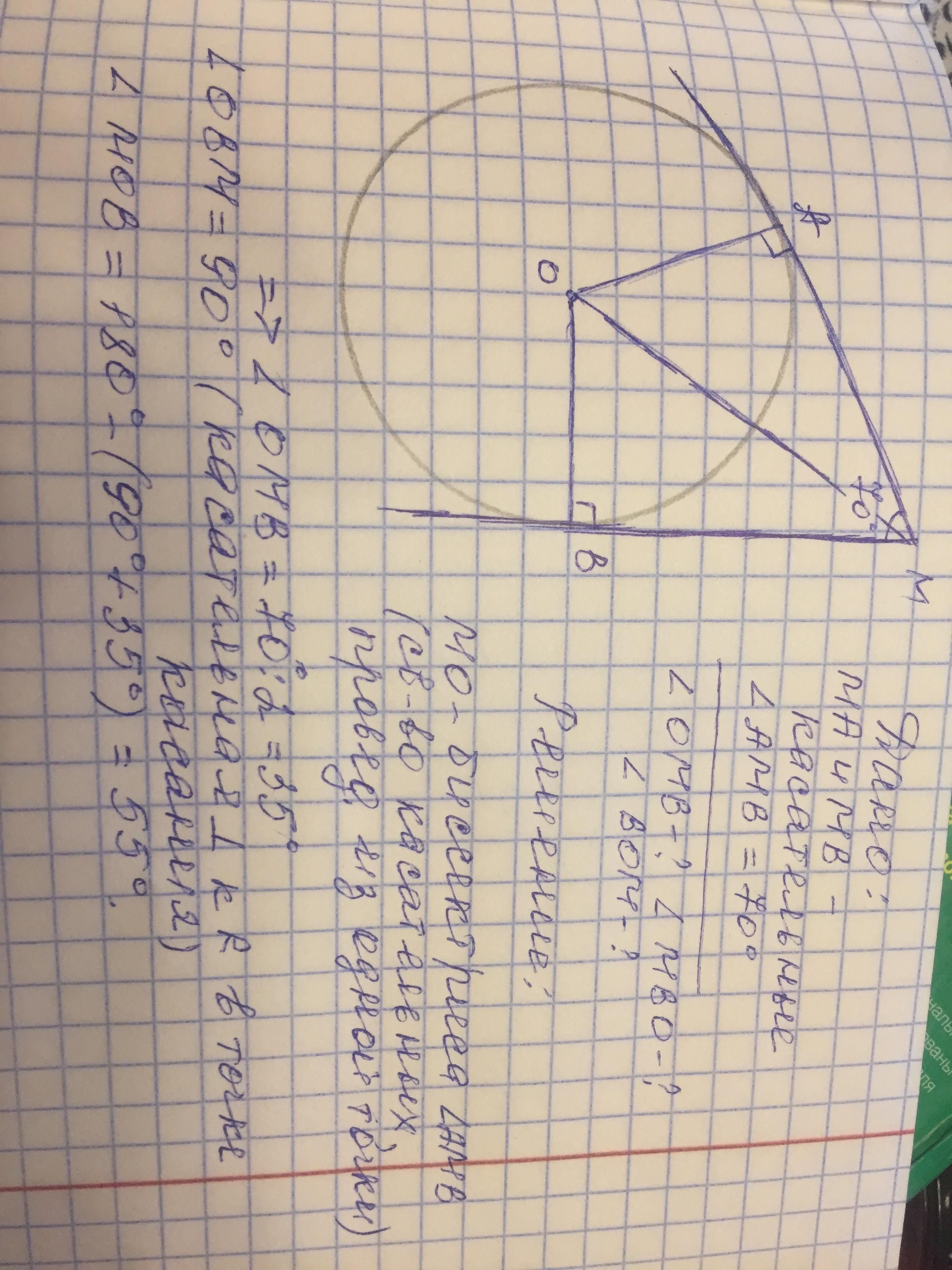
Из точки М к окружности с центром О проведены касательные МА и МВ,А и В- точки касания ,Угол АМВ=70 градусов !Найдите углы треугольника ОВМ
С РИСУНКОМ, С ДАНО И ВСЕ ПОДРОБНО ОПИСАНО ​

Answer 1

Ответ:

Геометрия=========================================

Объяснение:

Answer 2

спасибо большое

Answer 3

ПО свойству касательных, проведенных в точку касания, радиусы перпендикулярны касательным, точка О равноудалена от сторон угла АМВ, поэтому лежит на биссектрисе МО,  значит. ∠АМО=∠ВМО= 35°, ОА⊥МА, ОВ⊥МВ, поэтому равных в прямоуг. треугольниках АМО  и ВМО /ОМ- общая гипотенуза, катеты ОА=ОВ,   углы АОМ и ВОМ равны по 90°- 35°=55°

Итак, ))) в ΔОВМ

∠О=55°, ∠В=90°; ∠М=35°

Вроде ни о ком не забыл.))))