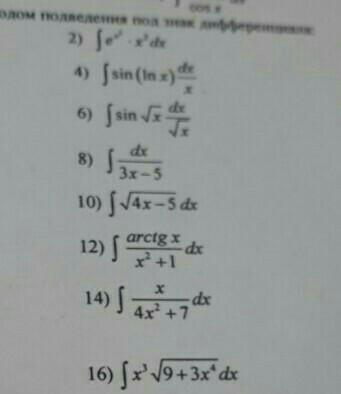Question

вычеслить интеграл методом подведения под знак дифференциала
помогите пожалуйста ​​

Answer 1

$2); ; int e^{x^6}, x^5, dx=[; d(x^6)=6x^5, dx; ]=frac{1}{6}int e^{x^6}, d(x^6)=frac{1}{6}e^{x^6}+C; ;\\4); ; int sin(lnx), frac{dx}{x}=[; d(lnx)=frac{dx}{x} ; ]=int sin(lnx), d(lnx)=-cos(lnx)+C; ;\\6); ; int sinsqrt{x}, frac{dx}{sqrt{x}}=[; d(sqrt{x})=frac{dx}{2sqrt{x}}; ]=2int sin(sqrt{x}), d(sqrt{x})=-2, cos(sqrt{x})+C; ;\\8); ; int frac{dx}{3x-5}=[; d(3x-5)=3, dx; ]=frac{1}{3}int frac{d(3x-5)}{3x-5}=frac{1}{3}, ln|3x-5|+C; ;$

$10); ; int sqrt{4x-5}, dx=[; d(4x-5)=4, dx; ]=frac{1}{4}int sqrt{4x-5}cdot d(4x-5)=\\=frac{1}{4}cdot frac{2cdot sqrt{(4x-5)^3}}{3}+C=frac{1}{6}cdot sqrt{(4x-5)^3}+C; ;\\12); ; int frac{arctgx}{x^2+1}=[; d(arctgx)=frac{dx}{1+x^2}; ]=int arctgx, d(arctgx)=frac{arctg^2x}{2}+C; ;\\14); ; int frac{x}{4x^2+7}, dx=[; d(4x^2+7)=8x, dx; ]=frac{1}{8}int frac{d(4x^2+7)}{4x^2+7}=frac{1}{8}, ln|4x^2+7|+C; ;\\16); ; int x^3sqrt{9+3x^4}, dx=[; d(9+3x^4)=12x^3, dx; ]=\\=frac{1}{12}int sqrt{9+3x^4}cdot d(9+3x^4)=frac{1}{12}cdot frac{2cdot sqrt{(9+3x^4)^3}}{3}+C=frac{1}{18}cdot sqrt{(9+3x^4)^3}+C; .$

Answer 2

...dt=t'dt...

Answer 3

Метод замены переменой типо... Настя смекалку включайте..

Answer 4

NNNLLL54 поможете с неравенствами? Последний вопрос в профиле... Буду очень Благодарен!

Answer 5

позже, сейчас уже некогда

Answer 6

Ок буду ждать, только не забудьте)