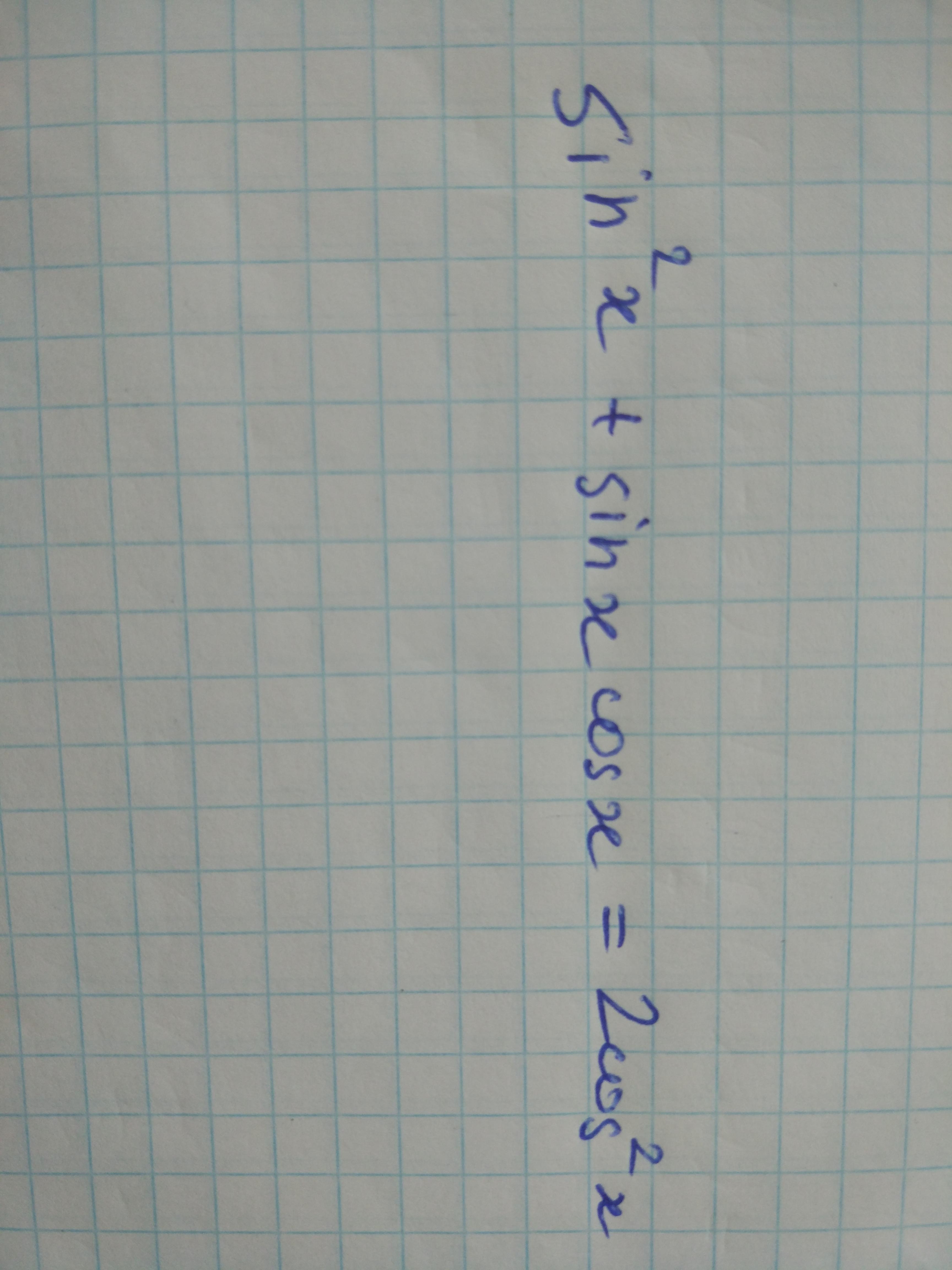Question

Тригонометрическое УРАВНЕНИЕ :
Sin^2x+sinxcosx=2cos^2x

Answer 1

sin²x - 2cos²x + sinx*cosx = 0

Поделим обе части на cos²x ≠ 0

tg²x + tgx - 2 = 0

Пусть t = tgx, t ∈R

t² + t - 2 = 0

t1 = -2 и t2 = 1

Обратная замена:

tgx = -2

tgx = 1

x₁ = - arctg(2) + pk, k∈Z

x₂ = p/4 + pn, n∈Z

Ответ: x₁ = - arctg(2) + pk, k∈Z

x₂ = p/4 + pn, n∈Z

Answer 2

отмечай как лучшее :)

Answer 3

А как ?

Answer 4

завтра кнопочка появится