Question

Доказать, что MRT=NST (прямоугольные треугольники)

Answer 1

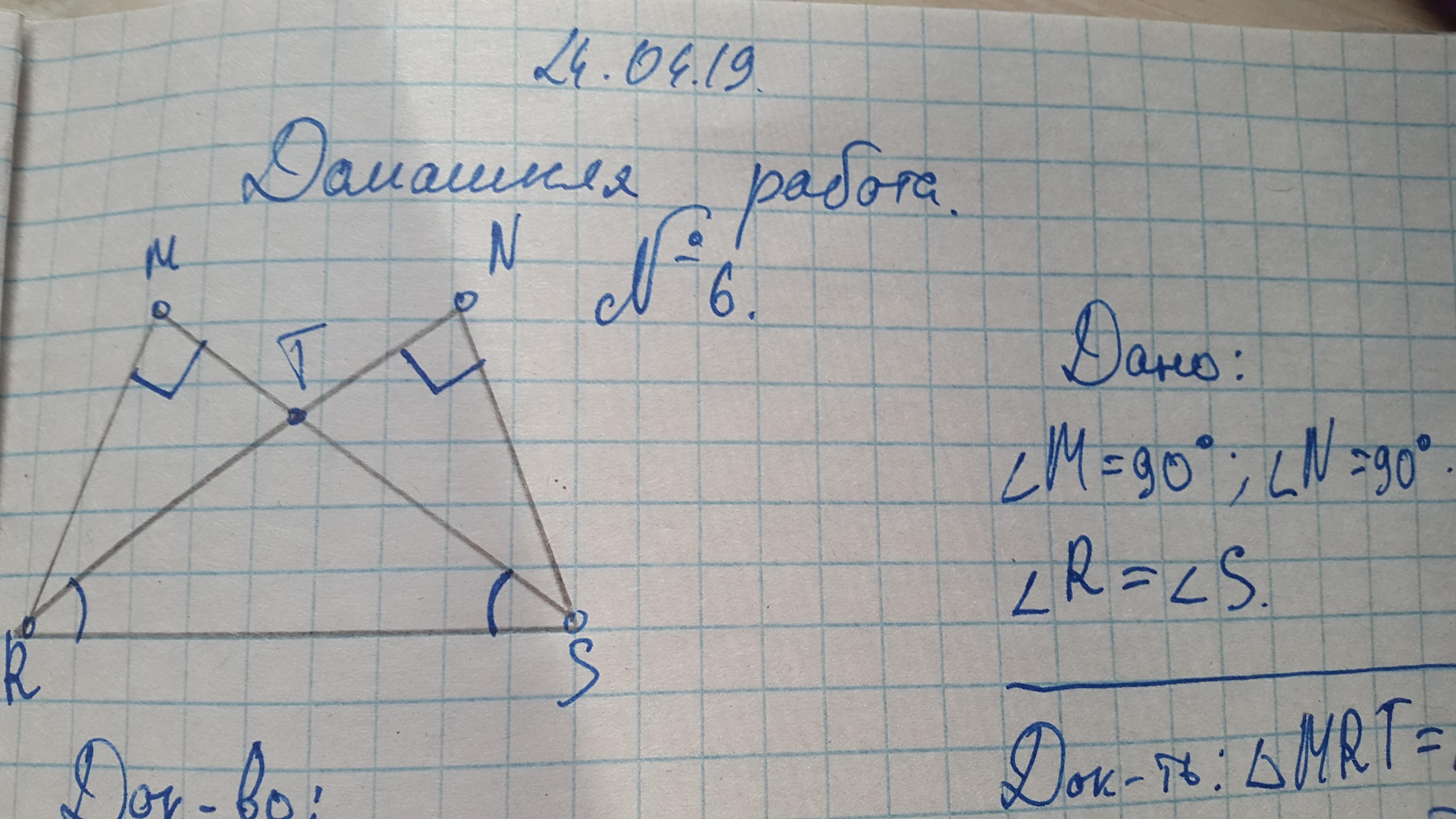
MSR=NRS(по общей гипотенузе RS и острым углам NRS и MSR)

MR=NS(как соответствующие элементы равных треугольников MSR и NRS)

Угол NTR= углу NTS(вертикальные)

Угол M и N=90°

Тогда MTR=NTS(по катету и противолежащему остром углу)

Answer 2

Ответ:

Доказательство:

У треугольников MRS и SNR гипотенуза общая и ∠NRS = ∠MSR. Следовательно, ΔMRS и ΔSNR равны по гипотенузе и острому углу (третий признак равенства прямоугольных треугольников)