Question

Точка А, взятая внутри двугранного угла, равного 120*, удалена от каждой из граней на а. Найдите угол между перпендикулярами из точки А на грани. Помогите, пожалуйста. И можно с рисунком, пожалуйста??

Answer 1

Ответ:

60°

Пошаговое объяснение:

1. Известно, что точка А удалена от каждой грани на одинаковое расстояние, это расстояние есть перпендикуляр к грани.

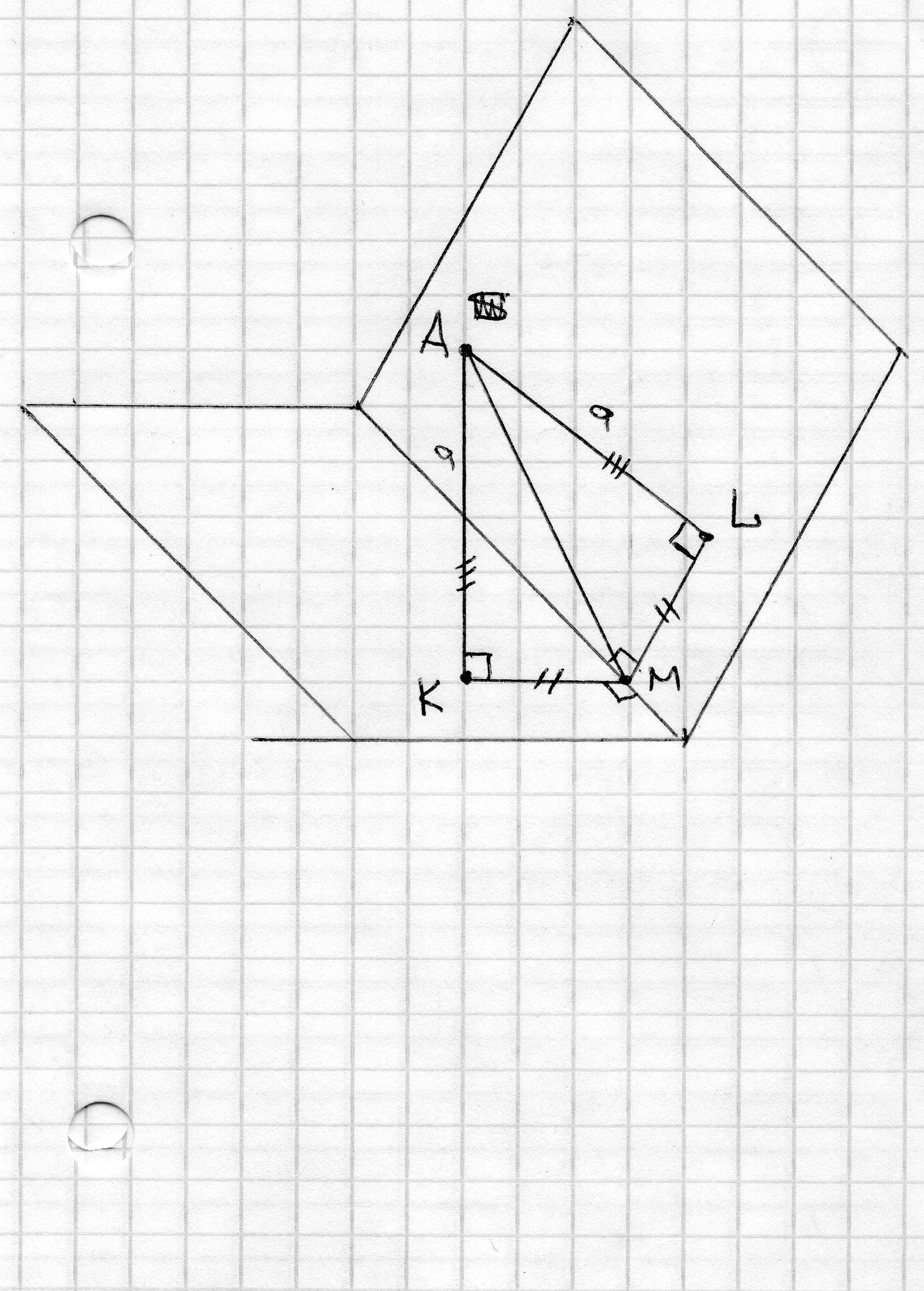
Строим указанные перпендикуляры, получаем точки K и L.

2. Получаем плоскость LAK, которая пересечет двухгранный угол по линиям KМ и LM, а ребро угла в точке M.

3. В полученном четырехугольнике LAKM угол KML равен 120°,  

   а углы AKM и ALM по 90°

4. Сумма всех углов многоугольника определяется формулой

180° * (n-2), где n - число углов многоугольника, в нашем случае n=4

Сумма углов четырехугольника будет равна 180 * (4-2) = 360°

Вычитая из этой суммы все имеющиеся углы, получаем угол LAK:

360-120-90-90 = 60°

Примечание: отрезок AM можно не строить, это я добавил для наглядности.