Question

AB-диаметр окружности, угол CAB=64°. Найдите градусную меру дуги АС​

Answer 1

Ответ:

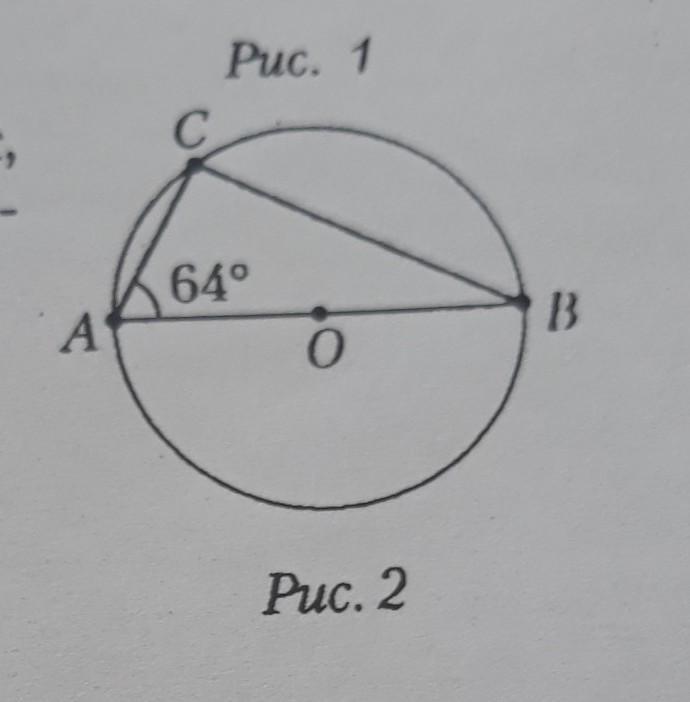
Сумма смежных углов равна 180°. Центральный угол равен половине вписанного.

x = 0.5(64°) = 32°.

y = 180° – 64° = 116°.

Пошаговое объяснение:

оставь коммент пж

Answer 2

Спасибо

Answer 3

Ответ:

Дуга АС = 52°

Пошаговое объяснение:

Известно, что AB-диаметр окружности и угол CAB=64°.

Так как AB диаметр окружности и вписанный угол ACB опирается на диаметр AB, то ∠ACB=90°. Сумма внутренних углов треугольника 180°, то есть

∠ACB + ∠CAB + ∠CBA = 180°.

Отсюда находим

∠CBA = 180° - ∠ACB - ∠CAB = 180° - 90° - 64° = 26°.

Вписанный угол равен половине дуги, на которую он опирается. Тогда величина дуги АС, на которую опирается вписанный угол CBA, два раз больше чем величина вписанного угла ∠CBA. Поэтому

дуга АС = 2·26° = 52°.