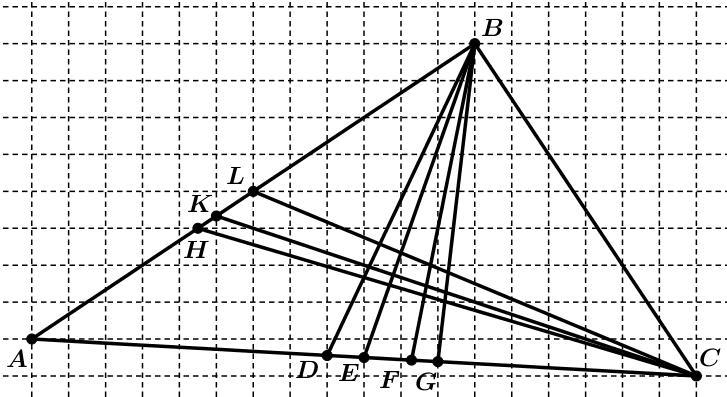
(СРОЧНО ДАЮ 30 БАЛЛОВ) Укажите точки, которые являются основаниями биссектрис треугольника ABC?
1)D
2) E
3) F
4) G
5) H
6) K
7) L
Ответы
Ответ:
Точка F - основание биссектрисы угла В треугольника АВС.
Объяснение:
Найдем по Пифагору стороны треугольника АВС (размеры по клеткам):
АВ = √(8² + 12²) = √208 ед.
ВС = √(9² + 6²) = √117 ед.
АС = √(18² + 1²) = √325 ед.
Выполняется равенство: АС² = АВ² + ВС², следовательно, треугольник АВС прямоугольный.
Так как биссектриса - это ГМТ, равноудаленных от сторон треугольника, то расстояния (перпендикуляры к сторонам) от точек L, K или H до сторон АС и ВС должны быть равны.
Но отрезок BL (перпендикуляр к ВС) больше перпендикуляра от точки L к стороне АC. Тем более отрезок КВ и НВ больше перпенндикуляров от точек К и Н к стороне АС. Следовательно, точки L, К и Н не могут быть основаниями биссектрисы угла С.
Рассмотрим точки D,E,F и G. Проведя перпендикуляры из этих точек к сторонам АВ и ВС (линии, параллельные этим сторонам), попробуем определить, который из получившихся прямоугольников может быть квадратом. Точки D и E - отпадают сразу, так как соседние стороны прямоугольников с вершинами в этих точках явно не равны.
Найдем по Пифагору отрезок ВМ ≈ √(5,1² + 3,4²) = √37,57 ед. Отрезок BN = √(5,1² + 3,4²) = √37,57 ед. С учетом погрешности измерений по клеткам, эти отрезки равны. Значит и отрезки FM и FN также равны (как противоположные стороны прямоугольника). Тогда FMBN - квадрат и точка F - основание биссектрисы угла В.
