Question

ПОМОГИТЕ ДАЮ 60 БАЛЛОВ ОЧЕНЬ СРОЧНО
В треугольнике ABC биссектрисы, проведенные из вершин B и С пересекаются в точке O. Прямая, проведенная через точку О, параллельно AB пересекает BC в точке E, а прямая, проведенная через точку OOO, параллельно АС пересекает ВС в точке DDD. Найдите длину OD, если OE=14,ED=16,BC=40

Answer 1

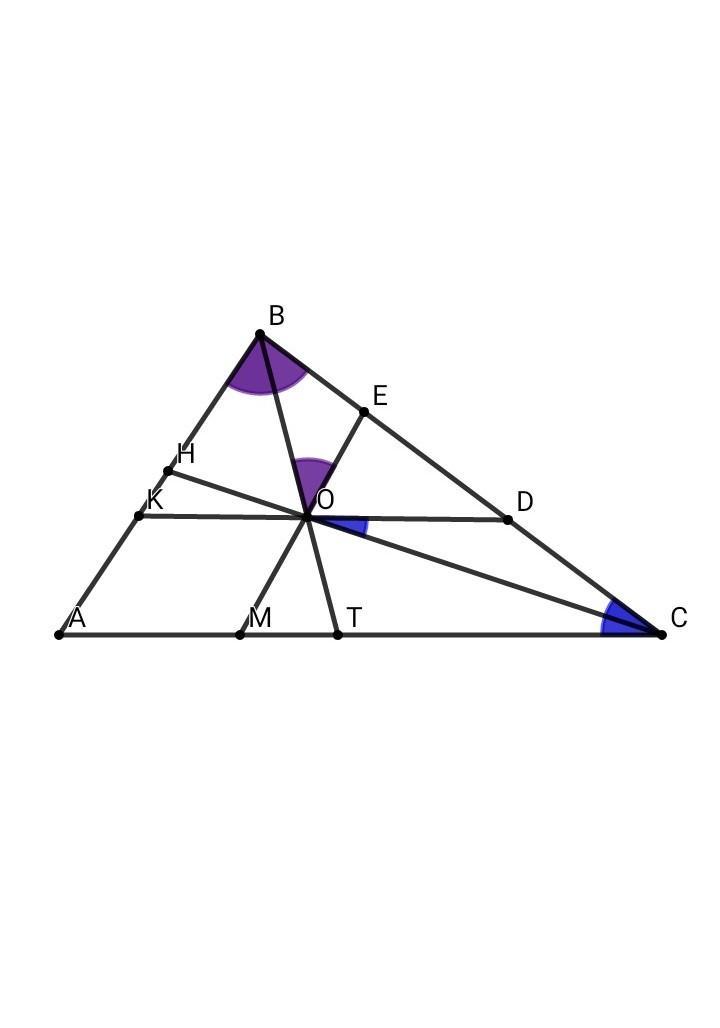
1. угол АСО = угол DCO, угол АСО = угол DOC - как накрест лежащие углы при KD || AC и секущей ОС. Значит, угол DCO = угол DOC => тр.DOC - равнобедренный, OD = DC.
2. Аналогично, тр. ВЕО - равнобедренный, ВЕ = ЕО = 14
3. DC = OD = BC - BE - ED = 40 - 14 - 16 = 40 - 30 = 10

ОТВЕТ: 10

Answer 2

Ответ:

Объяснение:

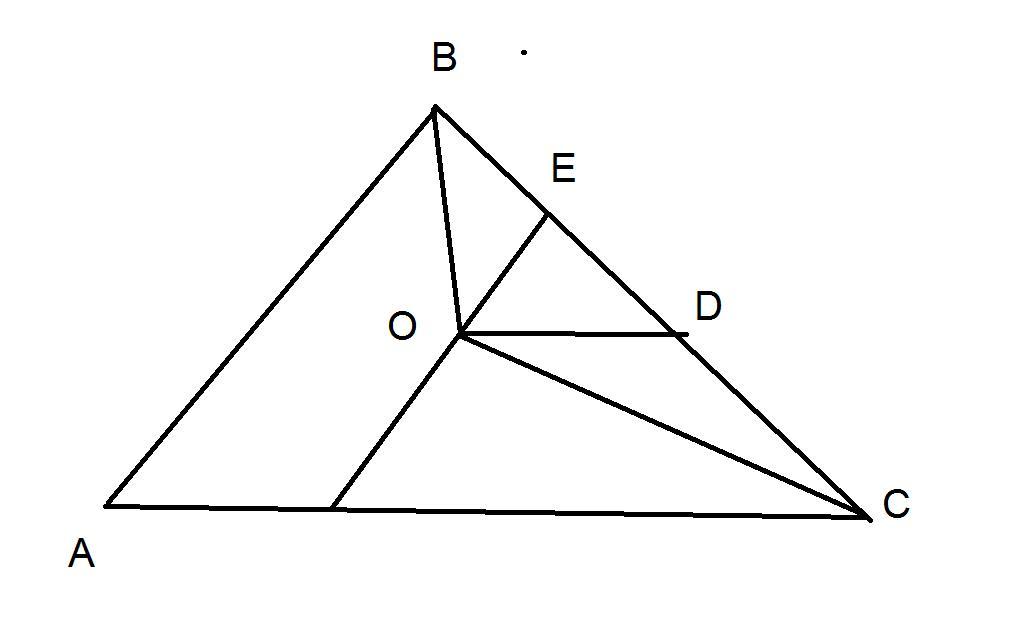
рассмотрим угол B

так как ВО - биссектриса  <АВО=<OВE

так как ОЕIIAB ⇒ <АВО=<BOE (внутренние накрест лежащие углы)

⇒<OВE=<BOE ⇒ ΔOВE - равнобедренный ⇒ BE=EO (1)

такие же рассуждения проведем для  угла С

рассмотрим угол С

так как СО - биссектриса  <DСО=<AСO

так как ОDIIAC ⇒ <DOC=<ACO (внутренние накрест лежащие углы)

⇒<DOC=<DCO ⇒ ΔDOC - равнобедренный ⇒ DO=DC (2)

(1),(2)⇒ РΔEOD=BC

BE=OE=14; ED=16

OD=DC=BC-BE-ED=40-14-16=10

OD=10

Answer 3

спасибо!