Question

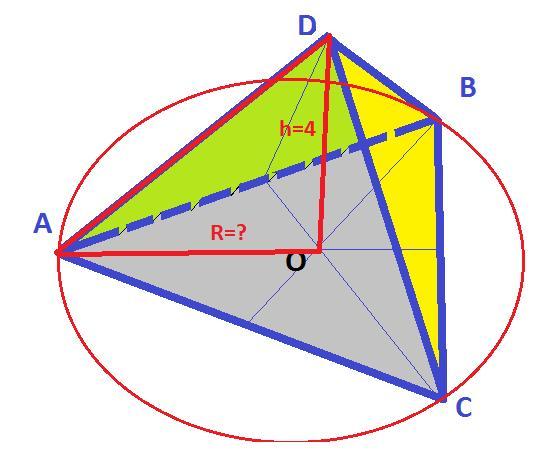
Стороны треугольника 10 см, 10 см и 12 см. Вне его плоскости находится точка на расстоянии 4 см от плоскости треугольника и на равном расстоянии от его вершин. Найти расстояние от этой точки до вершин треугольника

Answer 1

Пошаговое объяснение:

1 - находим радиус описанной окружности по формуле:

$R=frac{a*b*c}{4sqrt{p*(p-a)(p-b)(p-c)}}$

где: a,b и c - длины сторон треугольника, р = 1/2*(a+b+c).

Вычисляем:

р = 16, p-a = 6, p-b = 6, p-c = 4.

√(16*6*6*4) = √2304 = 48,  a*b*c = 10*10*12 = 1200

R = 6.25 - радиус окружности.

Теперь по теореме Пифагора находим расстояние до вершин.

a = 6.25, b= 4 - катеты. Находим гипотенузу.

с² = 6,25² + 4² = 16 + 39,0625 = 55,0625

с = √55,0625 ≈ 7,42 - расстояние до вершин - ответ.

Рисунок к задаче в приложении. Получаем пирамиду.