пожалуйста, помогите!!!
1. Исследуйте функцию у = х7 - 2х5 + х на четность
2. Найдите наименьшее значение функции и определите, при каких значениях х оно достигается
Приложения:
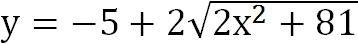
Ответы
Ответ дал:
0
Ответ:
Объяснение:
1. D(y)=(-∞;+∞) -симметричная
y(x)=x⁷-2x⁵+x
y(-x)=(-x)⁷-2(-x)⁵-x=-x⁷+2x⁵-x=-(x⁷-2x⁵+x)=-y(x) функция нечётная
2.y'=(-5+2√2x²+81)'=(-5)'+(2√2x²+81)'=2·4x/2√2x²+81=4x/√2x²+81
y'=0 знаменатель √2x²+81≠0 при любом x, значит 4x=0 x=0
на промежутке (-∞;0) производная <0 ⇒ функция убывает
на промежутке (0;+∞) производная >0 ⇒ функция возрастает
x=0 - точка минимума
y(0)=-5+2√2·0+81=-5+2√81=-5+18=13 - наименьшее значение функции
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад