Question

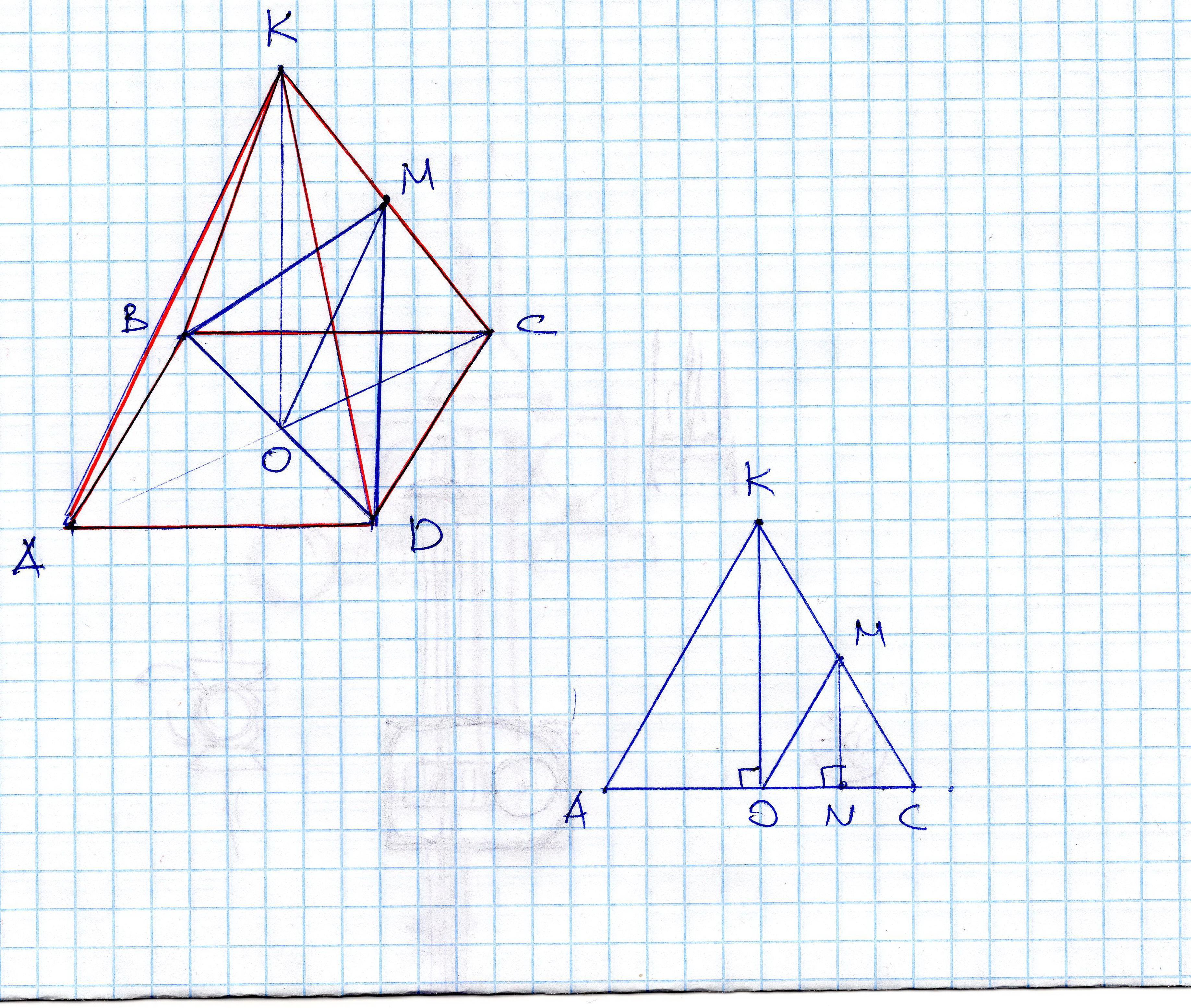
Основанием пирамиды, высота которой равна 12 дм, а боковые ребра равны друг другу, является прямоугольник со сторонами 6 дм и 8 дм. Найдите площадь сечения, проведенного через диагональ основания параллельно боковому ребру.

Огромное спасибо вам, когда поможете

Answer 1

Ответ:

50$sqrt{2644}$

Объяснение:

1. Найдем длину диагоналей прямоугольника, лежащего в основании пирамиды. По теореме Пифагора:

$AC^{2} =AB^{2} +BC^{2} \\AC = sqrt{AB^{2} +BC^{2}}= sqrt{64+36} =10$дм.

AO = AC/2= 100/2 = 5 дм

2. Для наглядности, начертим сечение по плоскости на которой лежит треугольник AKC

По теореме Фалеса (при пересечении угла параллельными прямыми стороны угла делятся на пропорциональные отрезки) видно, что параллельные прямые AK и OM делят AC и KC на пропорциональные отрезки, так как AO=OC=AC/2 (точка O середина диагонали), верно равенство КМ=MC=KC/2.

Аналогично прямые КО и MN делят ONC на равные отрезки

ON=NC

По признаку равенства прямоугольных треугольников, ΔONM = ΔCNM

(по двум катетам).

Вычислим KC по теореме Пифагора:

$KC=sqrt{KO^{2}+OC^{2} } = sqrt{12^{2}+5^{2}}=sqrt{169}=13$

Далее OM=MC=KC/2 = $13/2$

Площадь равнобедренного треугольника BMD равна половине произведения основания BD на высоту OM

S BDM = BD*OM = $10*13/2*1/2=5*13*1/2=32,5$

Answer 2

Большое спасибо

Answer 3

Не извлек один корень вначале, сейчас все верно и цифры стали красивые