Question

Срочно

40 баллов!!!!

Именно решение, не письменные объяснения, а формулы и решение.

Answer 1

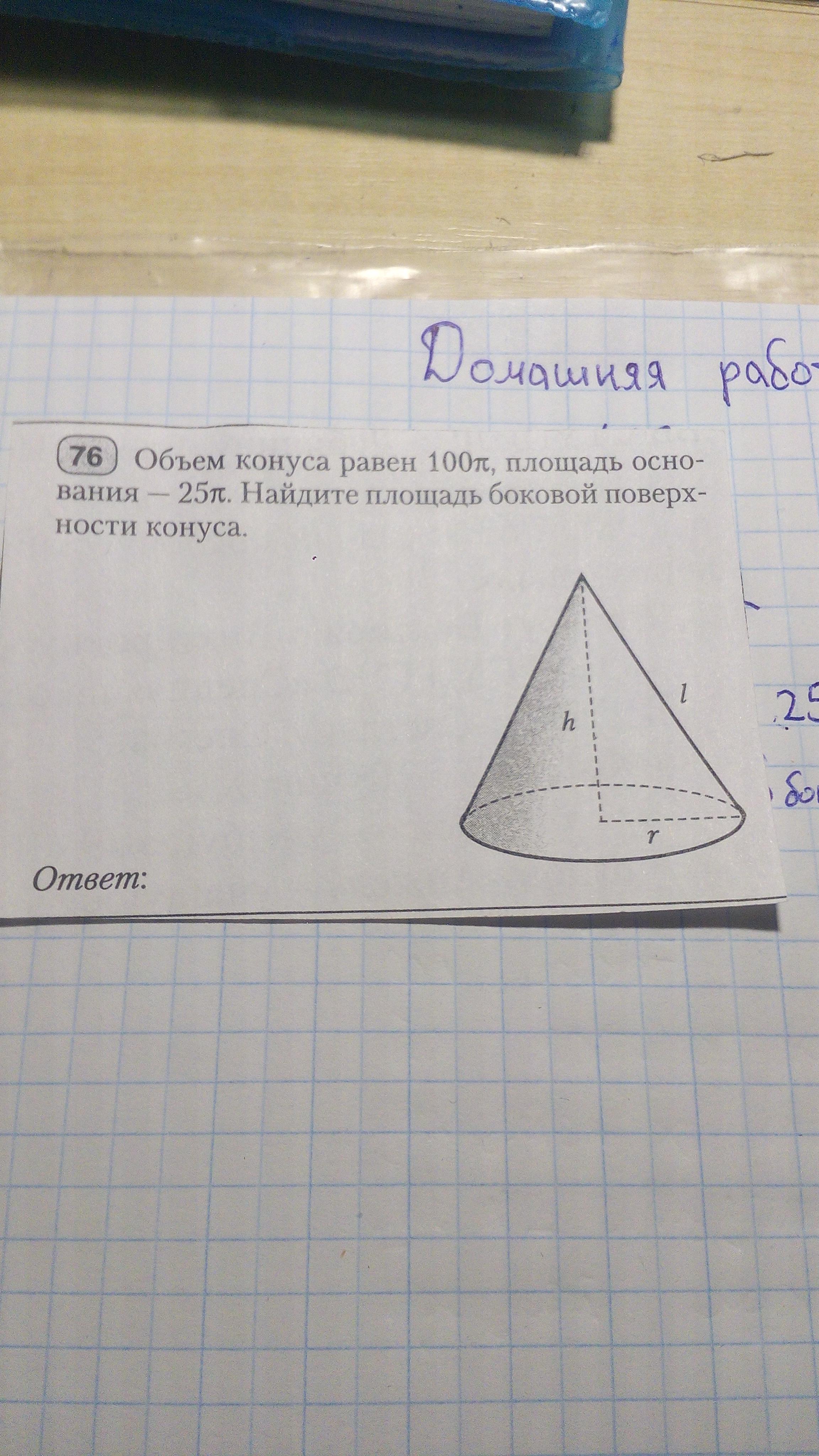
Площадь боковой поверхности конуса вычисляется по формуле
$s_{bpk} = pi{rl}$
где r-радиус основания, l-образующая.

Объем конуса
$v = frac{1}{3} pi{ {r}^{2} h}$
где h-высота конуса.

Основанием конуса служит круг и его площадь
$s_{kr} = pi{ {r}^{2} }$

1) Из формулы для площади круга найдем радиус основания:
$25pi = pi {r}^{2} \ {r}^{2} = 25 \ r = 5$
2) Из формулы объема конуса найдем высоту конуса
$100pi = frac{1}{3} pi times 25h \ h = frac{100 times 3}{25} \ h = 4 times3 \ h = 12$
3) Найдем образующую l по теореме Пифагора из прямоугольного треугольника, у которого катетами являются высота и радиус основания конуса, а гипотенузой - образующая конуса
${l}^{2} = {h}^{2} + {r}^{2} \ {l}^{2} = {12}^{2} + {5}^{2} \ {l}^{2} = 144 + 25 \ {l}^{2} = 169 \ l = 13$
4) Находим площадь боковой поверхности конуса
$s_{bpk} = pi times 5 times 13 \ s_{bpk} = 65pi$

Answer 2

Спасибо

Answer 3

Пожалуйста!

Answer 4

v=πr²h/3 - объем конуса

S=πr²=25π⇒r=5 радиус конуса

v=πr²h/3=100π⇒h=300/r²=300/25=12 высота конуса

l=√(h²+r²)=√(12²+5²)=13 - образующая конуса

S=πrl=5*13π=65π≈204,1 - площадь боковой поверхности

Answer 5

Спасибо