Ответы
Ответ дал:
0
Нужно привести к квадратному уравнению и решить его относительно переменной k
Теперь возведем обе части в квадрат:
И наконец решим уравнение относительно k:
Ответ дал:
0
Ответ:
Объяснение: решение в файле
Приложения:
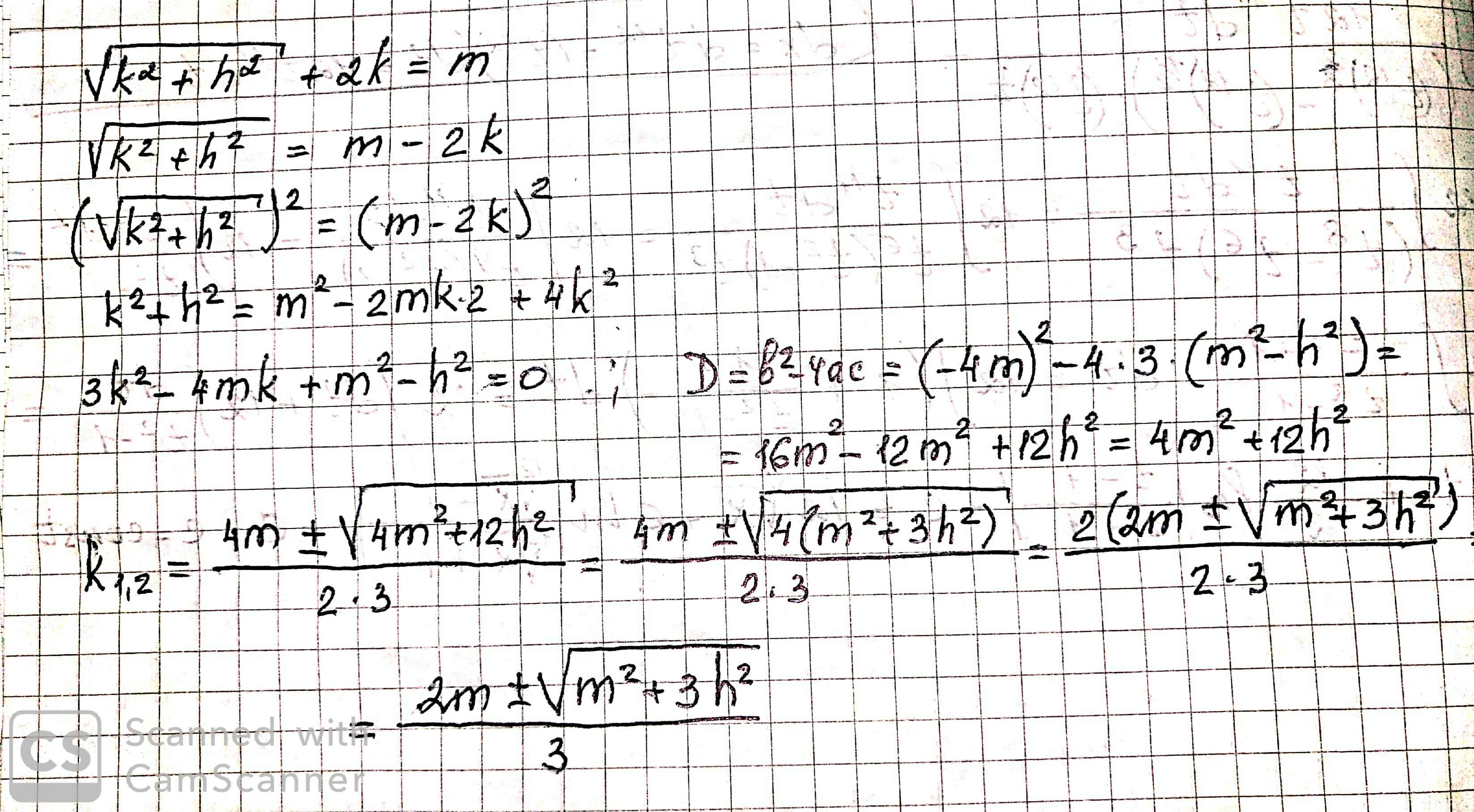
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад