Question

Дан прямоугольный треугольник FKM с прямым углом F и гипотенузой, равной 56. Известно, что площадь треугольника равна 392. Найди острые углы этого треугольника.

Answer 1

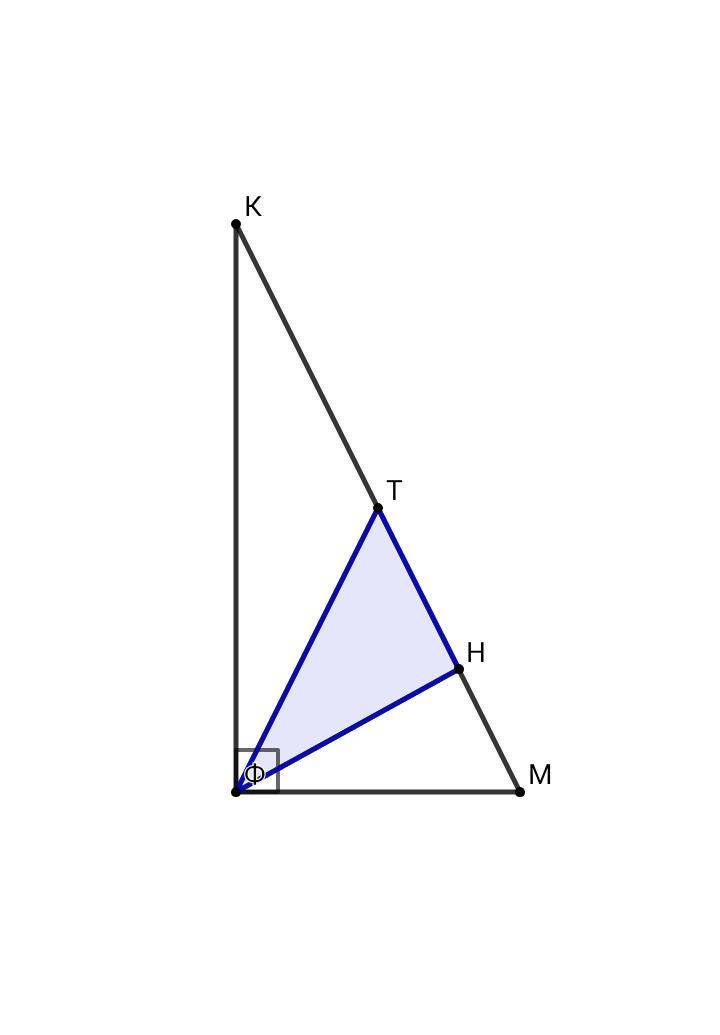
В прям.тр.FKM опустим из вершины прямого угла высоту и медиану

FT = KT = TM = 56/2 = 28 - по свойству прям.тр.

Площадь тр.FKM: S = (1/2)•KM•FH

392 = (1/2)•56•FH, FH = 14

В прям.тр.FTН: катет, лежащий против угла в 30°, равен половине гипотенузы. FН = FT/2, поэтому угол FTН = 30°

тр.FTM - равнобедренный (ВМ=МС):

угол TFM = угол TMF = (180° - 30°) : 2 = 75°

угол K = 90° - 75° = 15°

ОТВЕТ: 15° ; 75°

Answer 2

Ответ: 15° и 75°.

Объяснение: