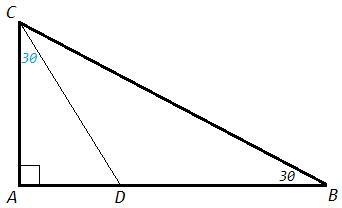
30 баллов. В прямоугольном треугольнике (∠A = 90°) величина угла B составляет 30°. Из вершины угла C проведена биссектриса CD, которая разбивает противоположный катет на отрезки AD и BD. докажите, что ∆ABC ~ ∆ACD; найдите отношение AD : BD.
Ответы
Ответ дал:
0
Сумма острых углов прямоугольного треугольника 90.
С=90-B=90-30=60
Биссектриса делит угол пополам.
ACD=C/2=60/2=30
Треугольники ABC и ACD подобны по двум углам.
Катет против угла 30 равен половине гипотенузы.
AC=BC/2
Биссектриса делит сторону в отношении прилежащих сторон (теорема о биссектрисе).
AD/BD = AC/BC =1/2
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад