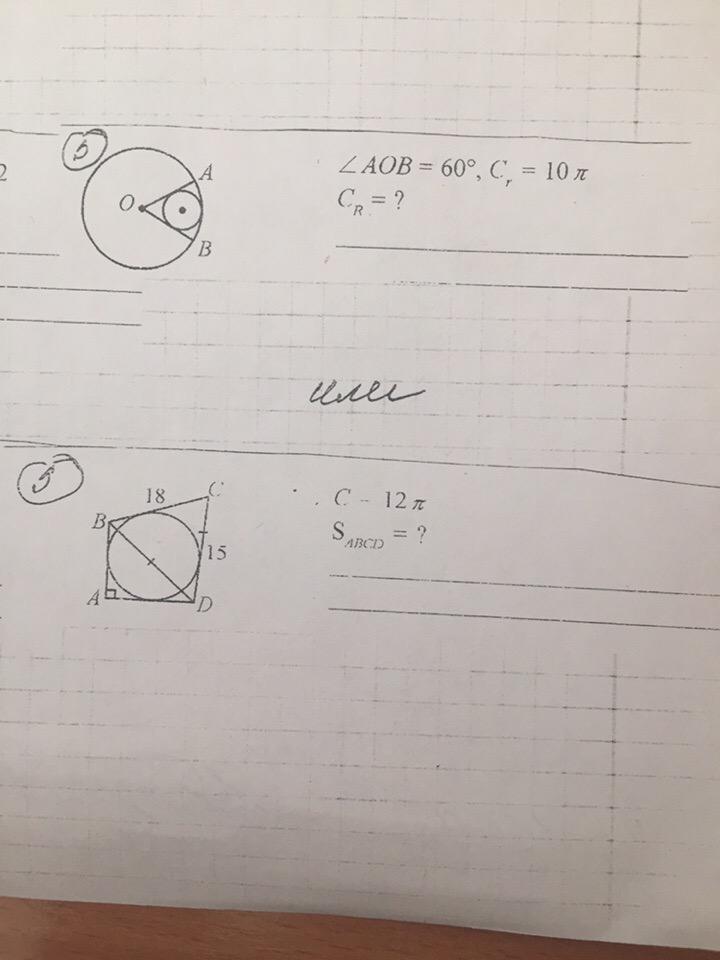Question

90 баллов решите плиз
хотя бы одну задачу

Answer 1

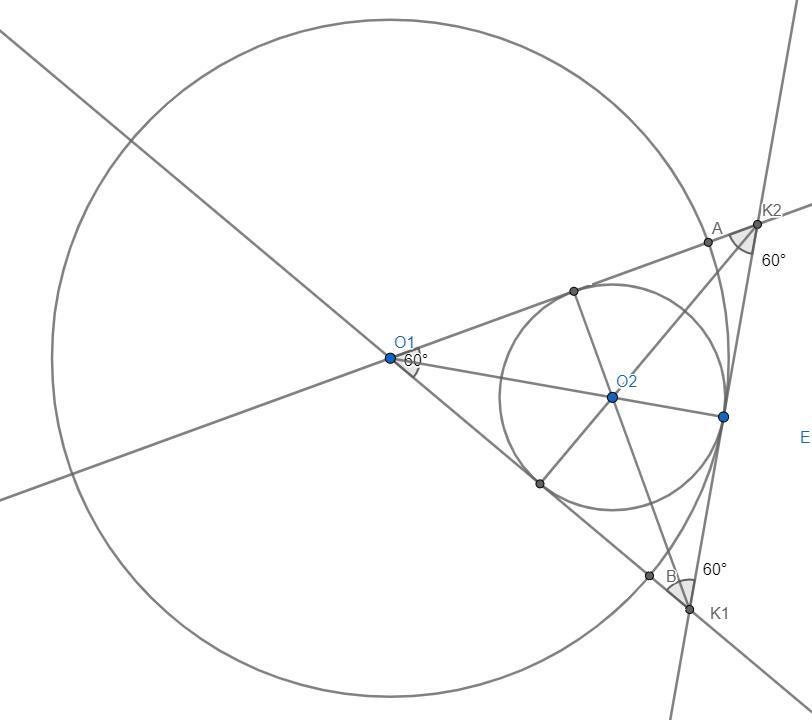
1)Проведем общую касательную к обеим окружностям и продлим стороны $O_1A$ и O1B до пересечения с общей касательной в точках K1 и K2.

Окружность с центром в точке O2 вписана в равносторонний треугольник $O_1K_1K_2$, и ее центр находится в точке пересечения биссектрис/медиан/высот.

Так как медианы в треугольнике делятся в отношении 2 к 1: радиус большой окружности в 3 раза больше радиуса малой.

$C_r=2pi r=10pi\r=5\R=5*3=15\C_R=30pi$

----------------------

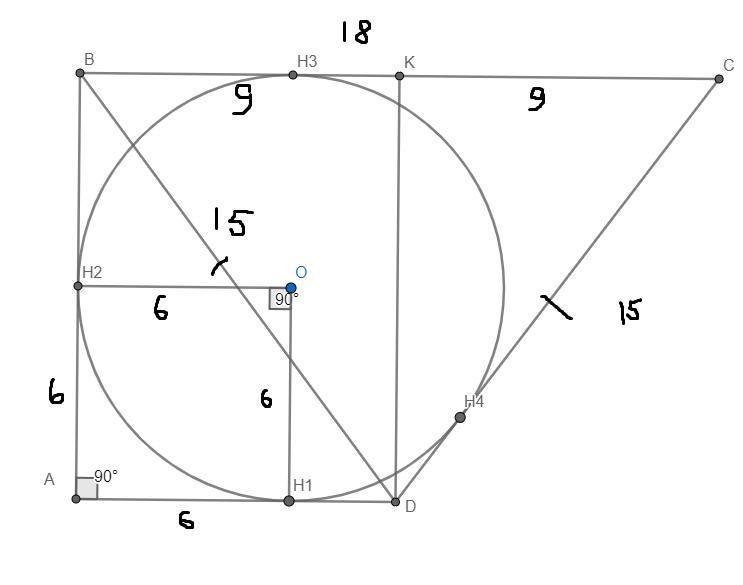
2) Рассмотрим четырехугольник $Ah_1h_2O$ он является квадратом так-как $Oh_1=Oh_2$ как радиусы и $Ah_1=Ah_2$ как отрезки касательных и все стороны пересекаются под прямым углом.

$C_r=2pi r=12pi\r=Ah_1=Ah_2=6$

Так как в четырехугольник вписана окружность- верно равенство

$15+r+h_2B=18+r+h_1D\h_2B=h_1D+3$

пусть $h_1D=x$ тогда по т. пифагора:

$(6+x)^2+(6+x+3)^2=15^2$

Отсюда $x=3$,

AD=9

AB=12

-----------

Опустим высоту в равнобедренном треугольнике BDC:

$cos(DBK)=frac{9}{15}$ так-как высота в равнобедренном треугольнике является медианой.

так-же заметим что $cos(BDA)=frac{9}{15}$

значит углы BDA и DBK равны.

значит прямые AD и BC || так как накрест лежащие углы при секущей BD равны.

значит четырехугольник ABCD- прямоугольная трапеция.

$S(ABCD)=frac{1}{2}*12*(18+9)=162$

------------------

Ответ: 1) $30pi$ 2) $162$