Решите систему линейных алгебраических уравнений
Тремя методами (метод Гаусса, метод Крамера,
Метод обратной матрицы)
Приложения:
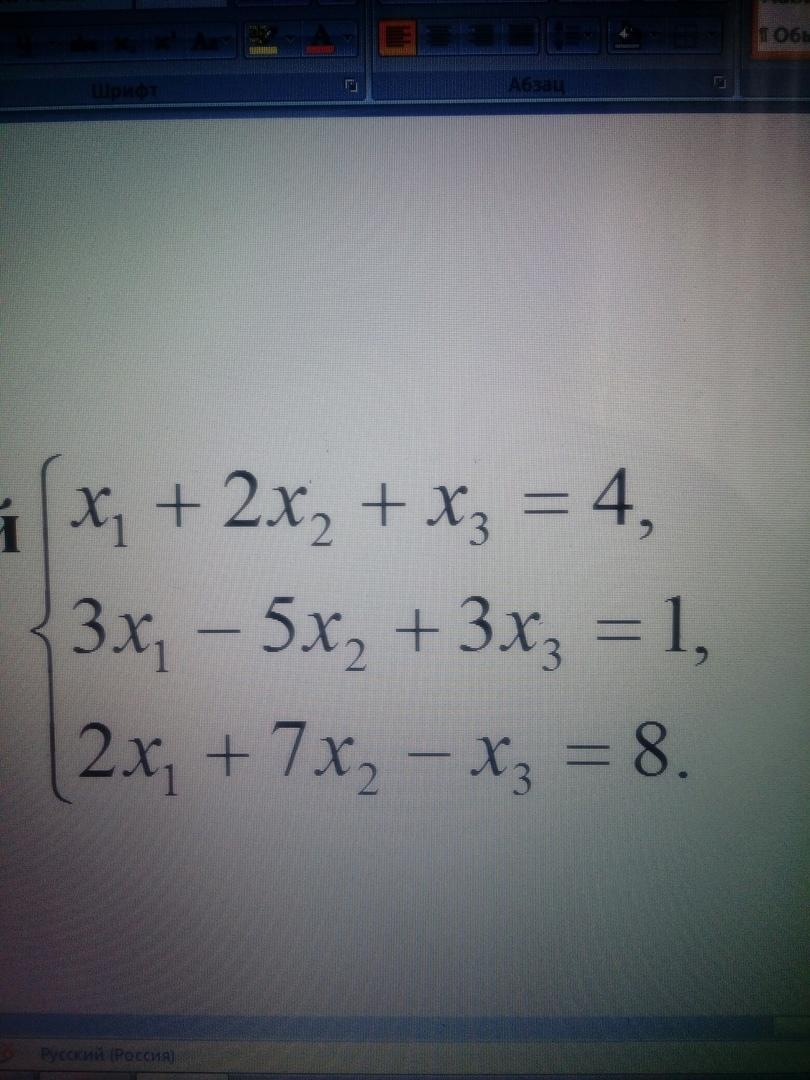
Ответы
Ответ дал:
0
Пошаговое объяснение:
1) Метод Гаусса:
2) Метод Крамера
3) Матричный метод
Вас заинтересует
2 года назад
2 года назад
9 лет назад
9 лет назад
10 лет назад