Question

Геометрия 7 класс.
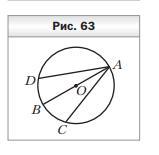
В окружности с центром О проведены диаметр АВ и хорды АС и AD, так что угол ВАС= углу BAD (рис. 63). Докажите, что AC=AD

Answer 1

В треугольниках АДВ и АСВ  углы САВ и ДАВ равны, например, α, т.к. их делит пополам биссектриса АВ, углы Д и С равны 90°, т.к. оба опираются на диметр АВ. тогда ∠АВС = ∠ АВД =90-α. Раз они равны, то и дуги на которые они опираются, тоже  равны, значит, дуга АС равна дуге АД, но тогда и  хорды, которые стягивают эти дуги, тоже равны. Значит,  АС=АД, что и требовалось доказать.