Вершины треугольника ABC делят описанную около него окружность на дуги AB, BC, CA, длины которых относятся как 3 : 4 : 5. Найдите радиус окружности, если меньшая из сторон треугольника равна 32.
Ответы
Ответ дал:
0
Пусть меньшая из дуг будет 3x тогда остальные дуги=4x и 5x соответственно.
Составим уравнение:
3x+4x+5x=360°
x=30°
значит меньшая дуга=90°, а меньший угол (лежащий напротив меньшей стороны) треугольника=45°
--------------
Из теоремы синусов:
Ответ:
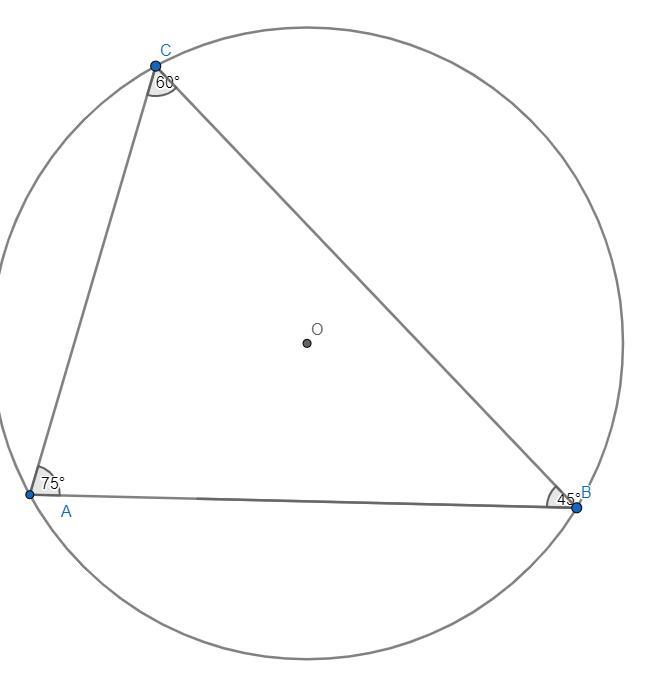
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад