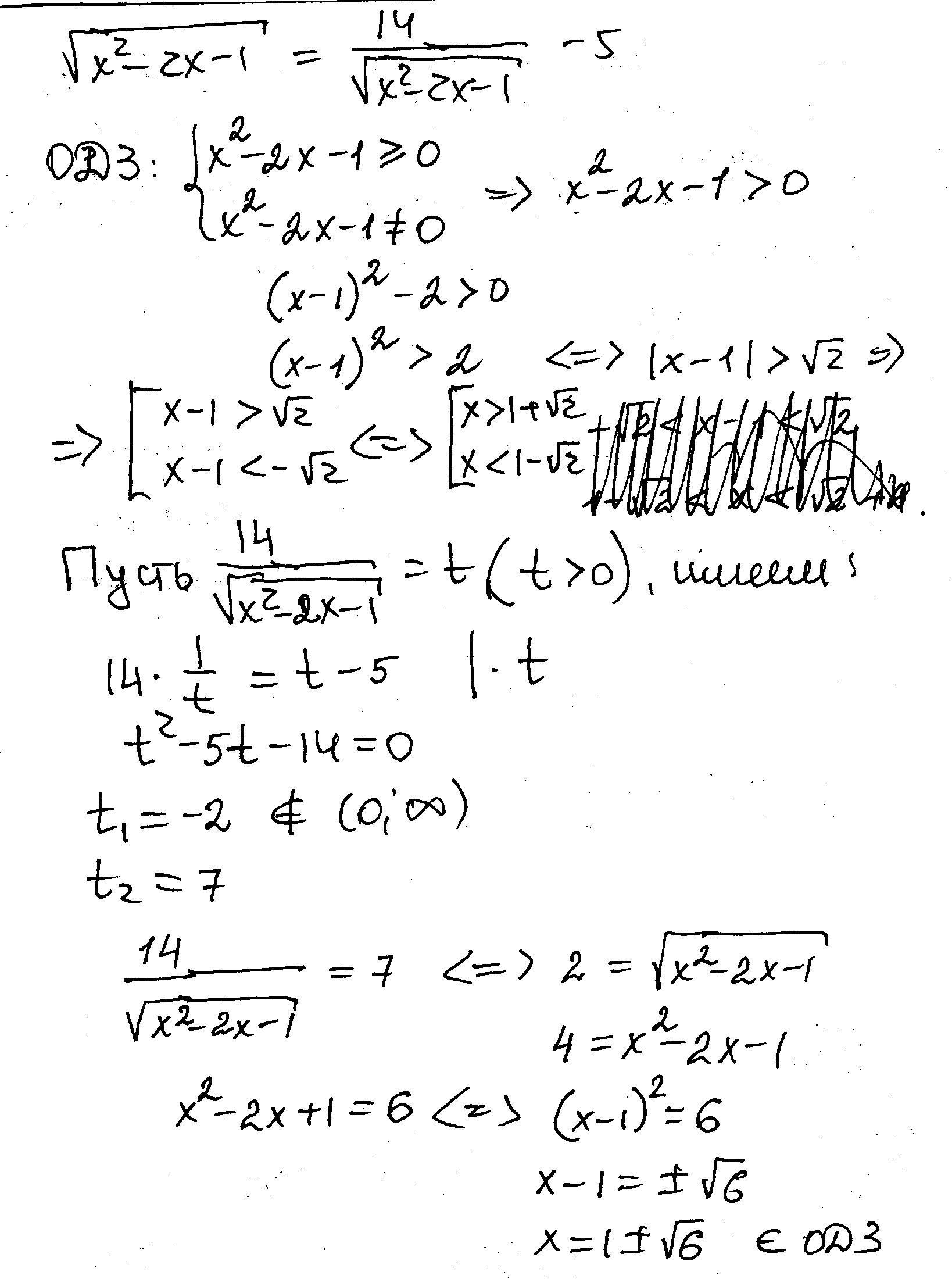Question

Помогите пожалуйста решить уравнение. 50 баллов

$sqrt{x^2-2x-1}=frac{14}{sqrt{x^2-2x-1} } -5$

Answer 1

Ответ: x = 1 ± √6.

Объяснение:

Дополнение к решению: проверка.

$sqrt{x^2-2x-1}=dfrac{14}{sqrt{x^2-2x-1}}-5\ \ sqrt{(x-1)^2-2}=dfrac{14}{sqrt{(x-1)^2-2}}-5$

Подставим найденные корни в уравнение

$sqrt{(1pmsqrt{6}-1)^2-2}=dfrac{14}{sqrt{(1pmsqrt{6}-1)^2-2}}-5\ \ sqrt{6-2}=dfrac{14}{sqrt{6-2}}-5~~~~Longleftrightarrow~~~~ 2=2$

Answer 2

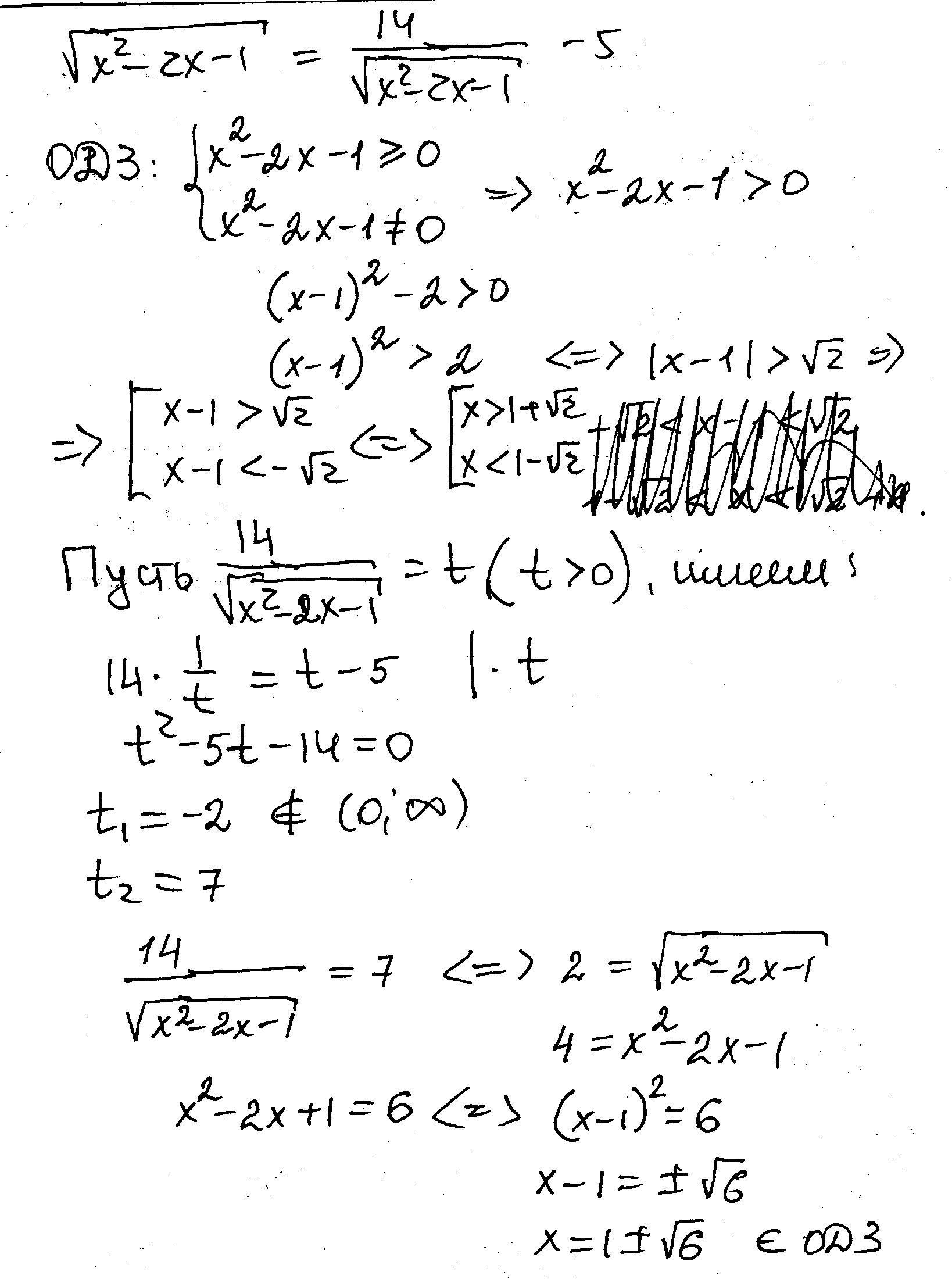
Корни квадратные существуют, когда подкоренные выражения в первом неотрицательные, во втором корне положительные, значит, ОДЗ уравнения - все значения, при которых х²-2х-1   >0, корнем левой части являются числа 1-√2 и 1+√2, которые разбивают область определения на три промежутка, в обл. определения попадают те, для которых подкоренное выражение строго больше нуля. Согласно методу интервалов , устанавливаем знаки, и выбираем те из них интервалы, которые дают положительный ответ,

это х∈(-∞;1-√2)∪(1+√2;+∞)

Пусть √(х²-2х-1)=в больше  нуля, тогда

в=14/в-5; в²+5в-14=0

По теореме, обратной теореме Виета, сумма корней -5, а произведение -14, это числа -7, но этот корень не может быть ответом, поскольку отрицательный, и число 2. Возвратимся к иксу.

√(х²-2х-1)=2, возведем обе части уравнения в квадрат, помня, что при этом могут появиться посторонние корни. Поэтому обязательно необходимо проверить полученные корни.

х²-2х-1=4,         х²-2х-5=0

х₁,₂=1±√6

Проверка. √((1+√6)²-2*(1+√6)-1)=√(1+2√6+6-2-2√6-1)=√4=2

Значит, левая часть равна двум, правая 14/2-5=2, указанный корень является корнем исходного уравнения, проверим второй корень.

Правая часть √((1-√6)²-2*(1-√6)-1)=√(1-2√6+6-2+2√6-1)=√4=2

Левая часть 14/2-5=2

Проверкой убедились, что оба корня являются корнями исходного уравнения.

Ответ. 1±√6