Question

Сформулируйте и докажите чему равен периметр треугольника,
образованного двумя касательными из одной точки и касательной,
проведенной к этой окружности через точку внутренней дуги.
(8 класс)

Answer 1

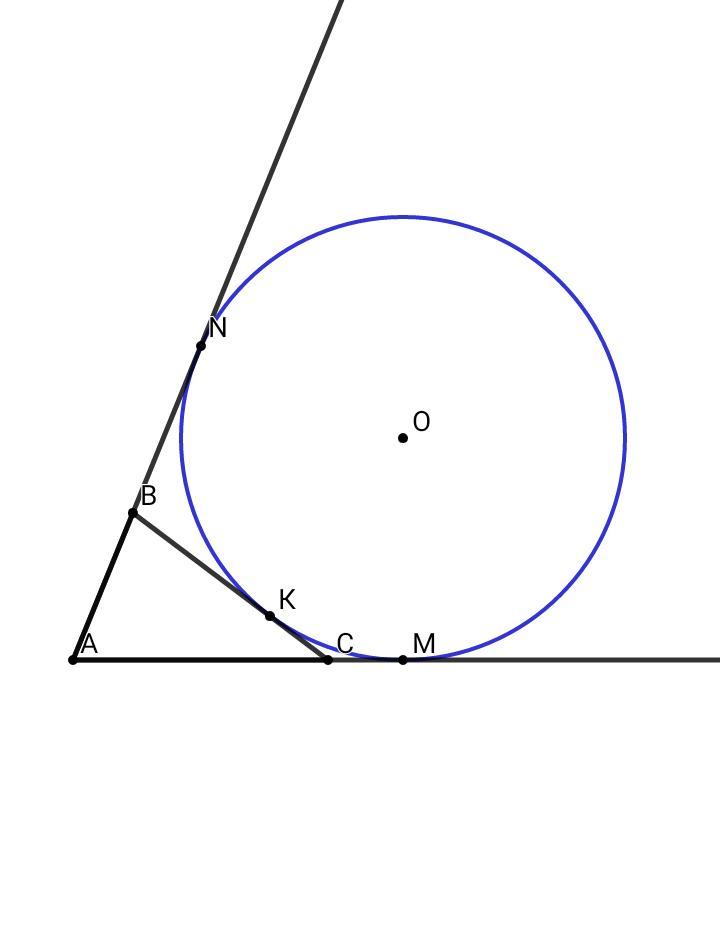
Отрезки касательных к окружности, проведенных из одной точки, равны

AN = AM , BN = BK , CM = CK

P abc = AB + AC + BC = AB + AC + (BK + CM) = AB + AC + (BN + CM) = (AB + BN) + (AC + CM) = AN + AМ = AM + AM = 2•AM

Значит, периметр треугольника, образованного двумя касательными из одной точки и касательной, проведённой к этой окружности через точку внутренней дуги, равен удвоенному бо'льшему отрезку его касательной