Question

Діагоналі трапеції ділять її на чотири трикутники.Довести,що трикутники,прилеглі до бічних сторін,є рівновеликими.ТЕРМІНОВОО!!!!!!!!!!!!!!!!!!!Будь ласка!!!!

Answer 1

Ответ:

Объяснение:

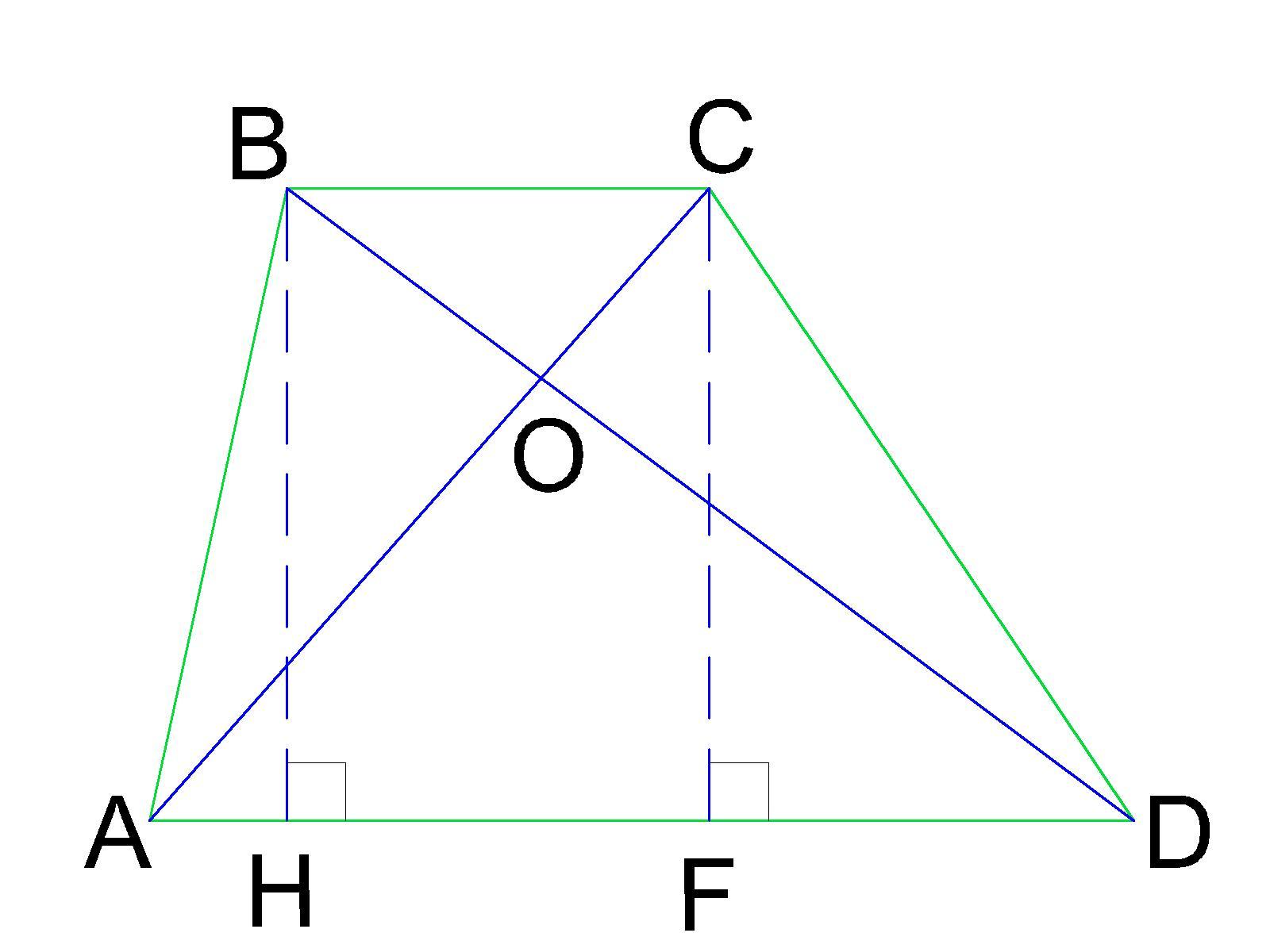
Побудуємо трапецію ABCD, та проведемо в ній діагоналі AС та BD, що перетинаються в точці О.

1) Проведемо в трикутниках ABD і ACD висоти BH і CF.

    $[{S_{Delta ABD}} = frac{1}{2}AD cdot BK,]$

   $[{S_{Delta ACD}} = frac{1}{2}AD cdot CF.]$

BK=CF (як висоти трапеції), відповідно,  

  $[{S_{Delta ABD}} = {S_{Delta ACD}}]$

2) Аналогічно доводимо рівність площ ΔABC та ΔBCD:

   $[{S_{Delta ABC}} = frac{1}{2}BC cdot BK,]$

   $[{S_{Delta BCD}} = frac{1}{2}BC cdot CF]$

та

   $[{S_{Delta ABC}} = {S_{Delta BCD}}]$

  $[{S_{Delta ABO}} = {S_{Delta ABD}} - {S_{Delta AOD}},]$

  $[{S_{Delta COD}} = {S_{Delta ACD}} - {S_{Delta AOD}}.]$

Так як площі трикутників ABD и ACD рівні (по вищедоведеному), то й

   $[{S_{Delta ABO}} = {S_{Delta COD}}]$

Таким чином, трикутники, утворені бічними сторонами та діагоналями трапеції, рівновеликі.