Question

Биссектрисы двух углов треугольника пересекаются под углом 70°. Сколько граду-

сов составляет величина третьего угла треугольника?​

Answer 1

Ответ:

Третий угол треугольника равен 40°.

Объяснение:

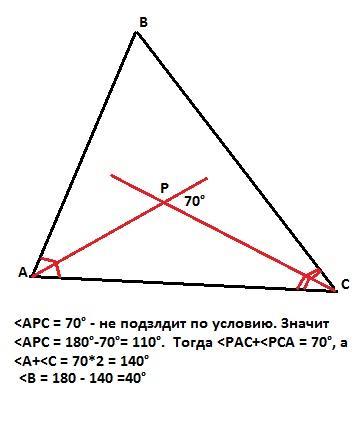
Пусть в треугольнике АВС биссектрисы углов А и С пересекаются в точке Р. Тогда, если угол между биссектрисами АРС равен 70°, то на сумму двух других углов в треугольнике АРС остается 180-70 = 110°.

Это сумма половин углов А и С треугольника АВС. Тогда сумма углов А и С должна быть равна 220°, что противоречит свойству треугольника: сумма внутренних углов должна быть равна 180°.

Следовательно, нам дан угол между биссектрисами, смежный с углом АРС, то есть угол АРС = 180° - 70° = 110°. И тогда сумма половин углов А и С равна 70°, сумма целых углов А и С равна 140°, а третий угол треугольника АВС равен 180° - 140° = 40° (по сумме внутренних углов треугольника).

Answer 2

Спасибо