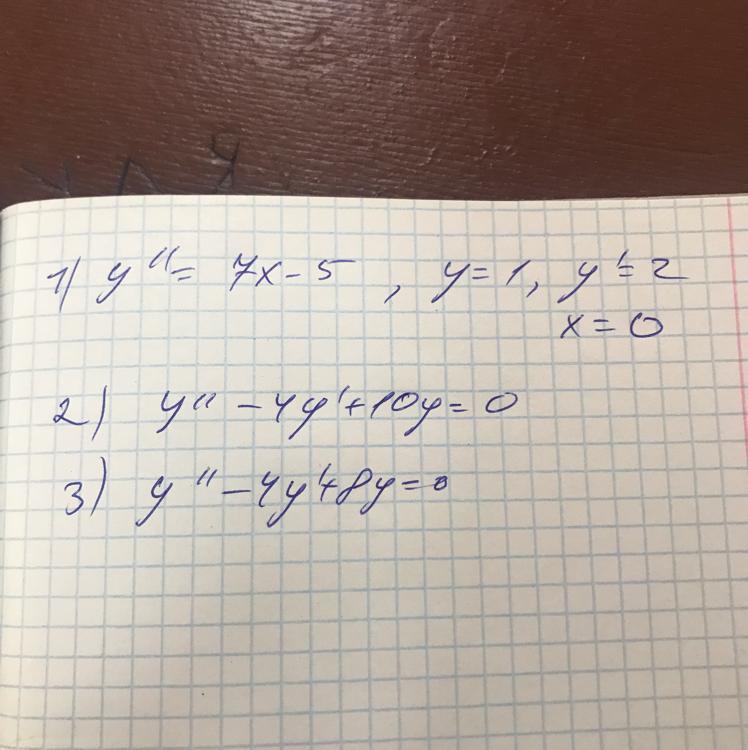Question

Дифференциальные уравнения второго порядка прошу надо срочно ребят

Answer 1

Объяснение:

1) Дважды почленно проинтегрируем обе части уравнения

$y'=displaystyle int (7x-5)dx=dfrac{7x^2}{2}-5x+C_1\ \ y=int left(dfrac{7x^2}{2}-5x+C_1right)dx=dfrac{7x^3}{6}-dfrac{5x^2}{2}+C_1x+C_2$

Подставив начальные условия, получаем систему уравнений

$displaystyle left { {{C_1=2} atop {C_2=1}} right.$

Частное решение задачи Коши: $y=dfrac{7x^3}{6}-dfrac{5x^2}{2}+2x+1$

2) Однородное дифференциальное уравнение с постоянными коэффициентами. Пологая $y=e^{kx}$, получим характеристическое уравнение

$k^2-4k+10=0~~~Longleftrightarrow~~~ (k-2)^2+6=0~~~Longleftrightarrow~~~ k=2pm isqrt{6}$

Общее решение: $y=e^{2x}left(C_1cossqrt{6}x+C_2sinsqrt{6}xright)$

3) Аналогично примеру 2), составить характеристическое уравнение

$k^2-4k+8=0~~~Longleftrightarrow~~~ (k-2)^2+4=0~~~Longleftrightarrow~~~ k=2pm 2i$

Общее решение: $y=e^{2x}left(C_1cos 2x+C_2sin 2xright)$