Ответы
Ответ дал:
0
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
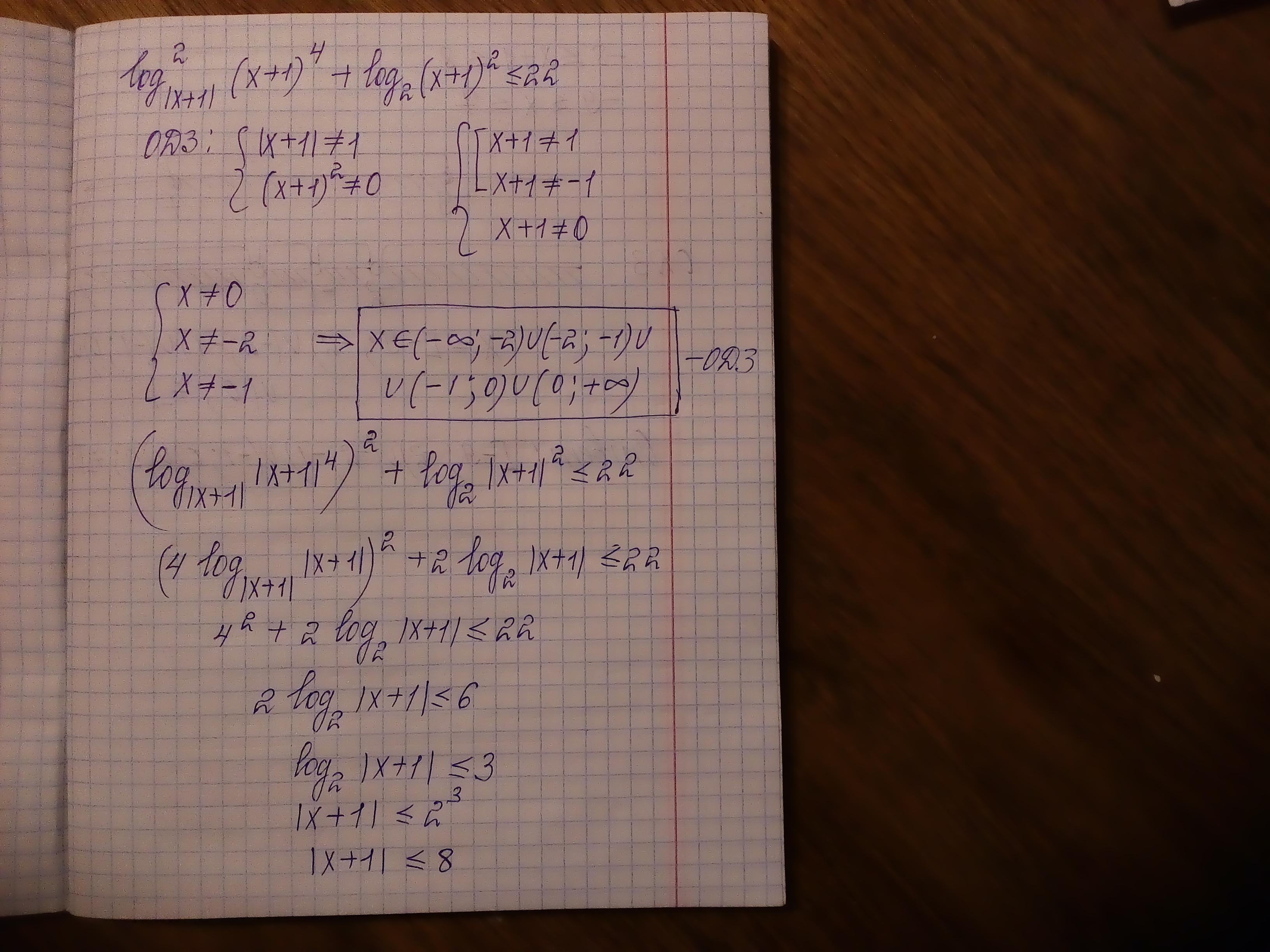

Ответ дал:
0
Ну ты голова, спасибо!
Ответ дал:
0
а ты можешь расписать одз поподробней, пожалуйста? заранее спасибо
Ответ дал:
0
Обновите страницу. Добавлено третье фото по поводу ОДЗ.
Ответ дал:
0
Заметим что
(x+1)^2n = |x+1|^2n переменная в четной степени, и модуль переменной в той же степени равны
Разберемся с первым членом
|x+1|^4 = (x+1)^4
ОДЗ |x+1|>0 х≠-1
|x+1|≠1 x≠0 x≠-2
log^2 (|x+1|) ( |x+1|)^4 = 4^2 = 16
16 + log(2) (x+1)^2 ≤ 22
log(2) (x+1)^2 ≤ log(2) 2^6
(x+1)^2 ≤ 2^6
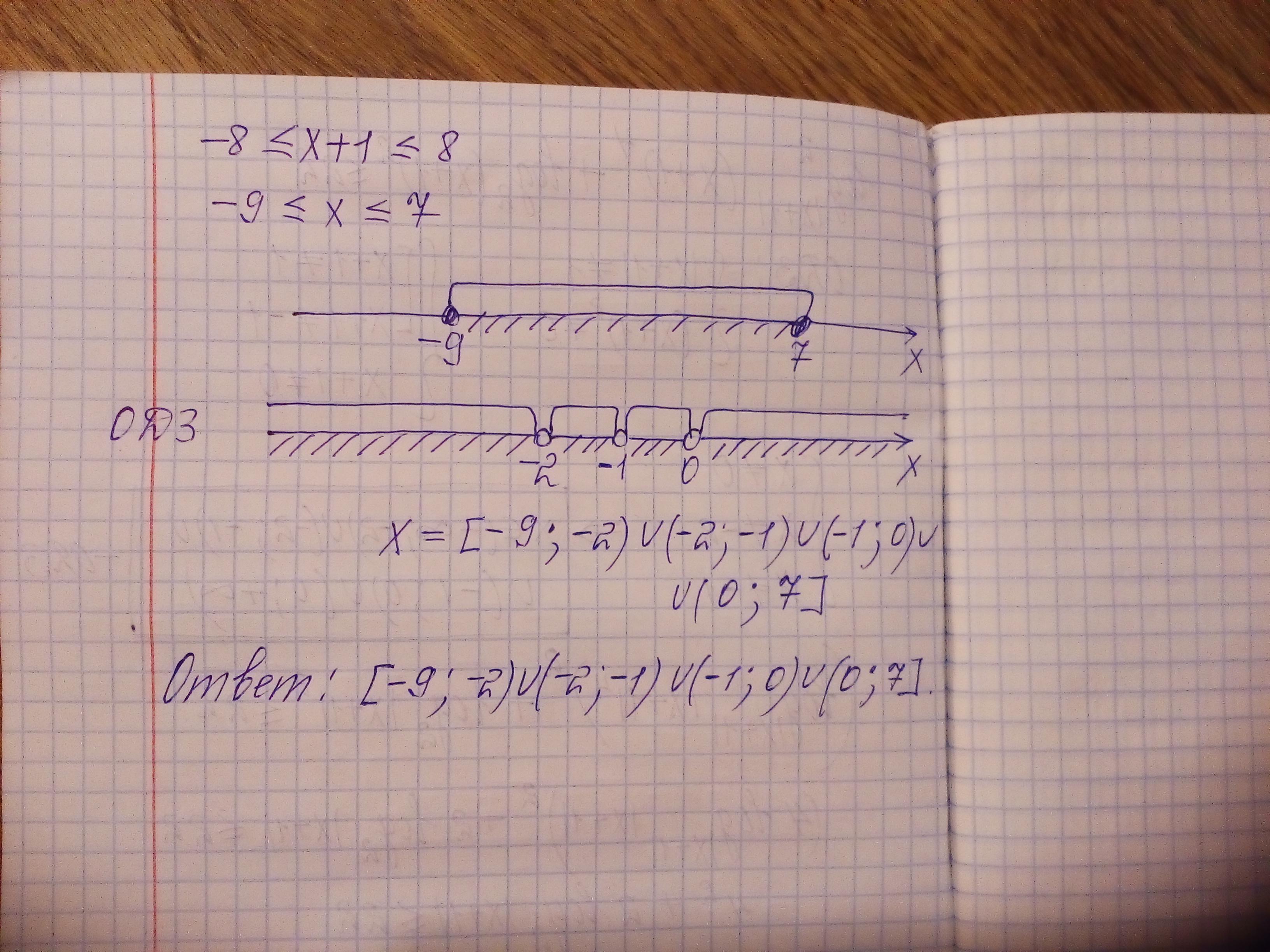
-2^3 ≤ x+1 ≤ 2^3
-9 ≤ x ≤ 7 смотрим ОДЗ
x∈ [-9 -2) U (-2 -1) U (-1 0) U (0 7]
Приложения:
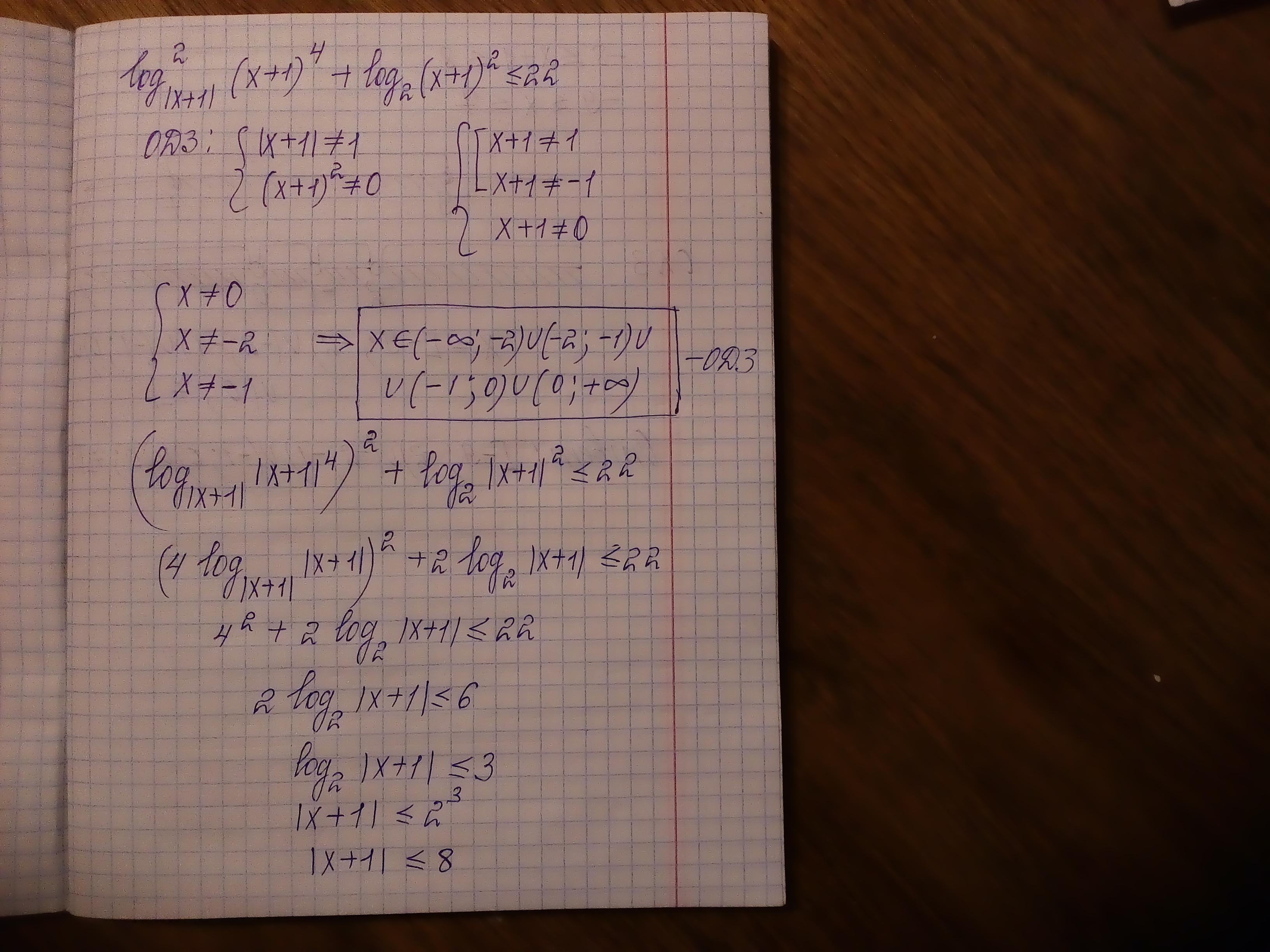


Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад