Question

Помогите решить задачу!

Две окружности, радиусы которых равны r и 3r, касаются внешне в точке K. К этим окружностям провели общую внешнюю касательную MN (точка M принадлежит большей окружности, точка N — меньшей).

1) Докажите, что центры этих окружностей и точка их касания K лежат на одной прямой.

2) Вычислите площадь фигуры KMN, ограниченной меньшими дугами ∪KM и ∪KN этих окружностей и отрезком MN.

Answer 1

1) Отразим рисунок относительно прямой AB, окружности перейдут сами в себя, а K – перейдёт в точку K', симметричную относительно прямой AB. Если K не лежит на AB, то K и K' не совпадают, и K' – тоже точка касания, чего быть не может.

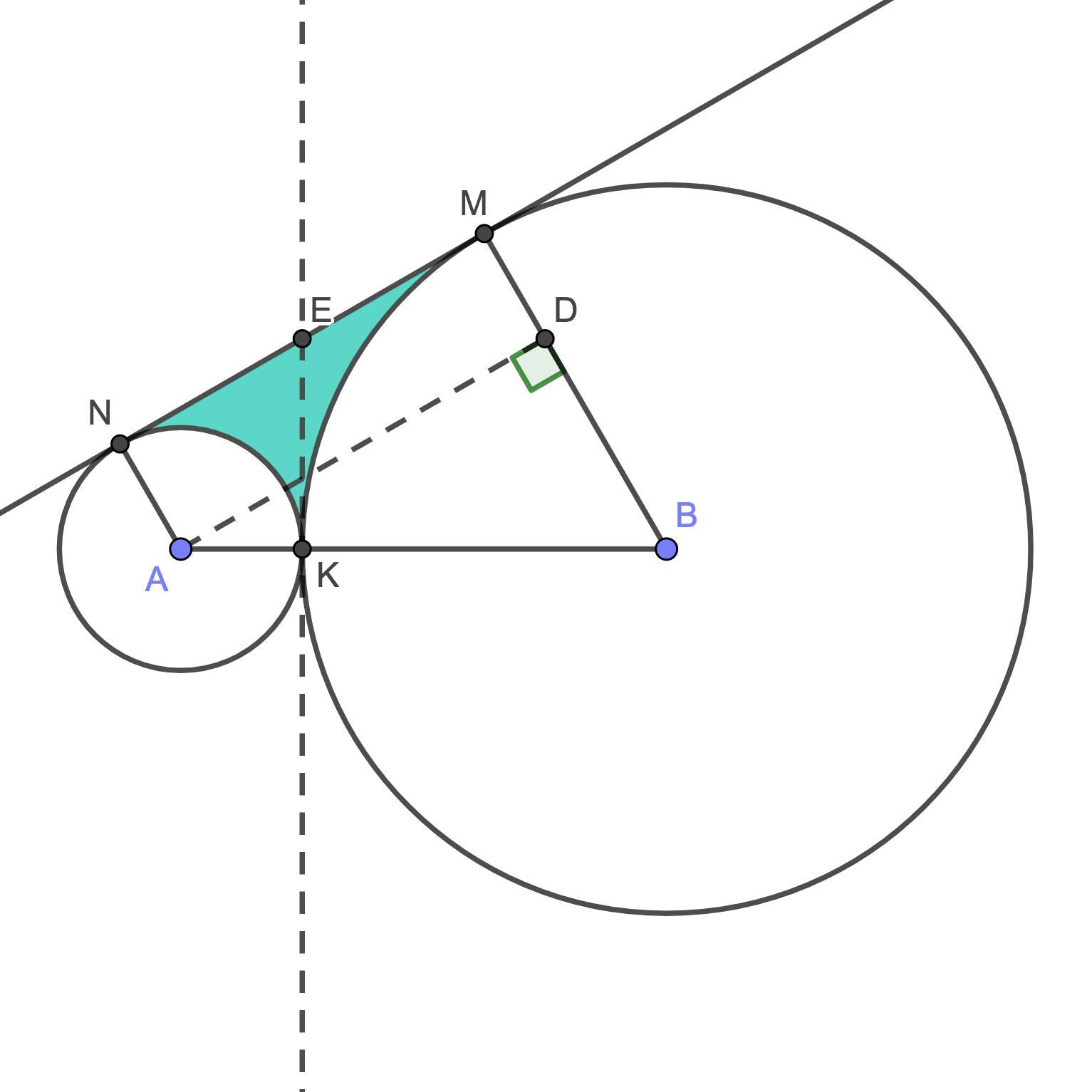
2) Радиусы, проведённые в точку касания, перпендикулярны касательной, поэтому AN и BM перпендикулярны NM, а тогда параллельны, ANMB – прямоугольная трапеция.

Проведём высоту трапеции AD. ANMD – прямоугольник, поэтому MD = AN = r, тогда BD = 2r. Кроме того, AB = AK + KB = 4r, поэтому ∠DAB = 30° (противолежащий катет равен половине гипотенузы), а по теореме Пифагора $AD=sqrt{AB^2-BD^2}=2sqrt3r$.

Площадь трапеции ANMB равна $(AN + MB) cdot AD / 2 = 4sqrt3r^2$

Площадь сектора KAN с центральным углом 90° + 30° = 120° = π/3 равна $pi r^2/3$

Площадь сектора KBM с центральным углом 90° - 30° = 60° = π/6 равна $pi(3r)^2/6=3pi r^2/2$

Площадь искомой фигуры

$4sqrt3r^2-dfrac{pi r^2}{3}-dfrac{3pi r^2}2=left(4sqrt3-dfrac{11pi}6right)r^2$

Answer 2

Спасибо!