В правильной треугольной пирамиде SABC с основанием ABC известны ребра: AB=8√3, SC=17.
Найдите угол, образованный плоскостью основания и прямой AM, где M - точка пересечения медиан грани SBC/
(пожалуйста, с рисунком)
Ответы
Ответ дал:
0
пусть точка K середина стороны BC.
AK- медиана/биссектриса/высота в равностороннем треугольнике ABC.
найдем AK:
----------------------
SK- медиана/биссектриса/высота в равнобедренном треугольнике SBC.
найдем SK:
по теореме пифагора:
(так как точка пересечения медиан делит их в отношении 2 к 1)
значит искомый угол равен:
что приблизительно равно 23,32701352...°
Приложения:
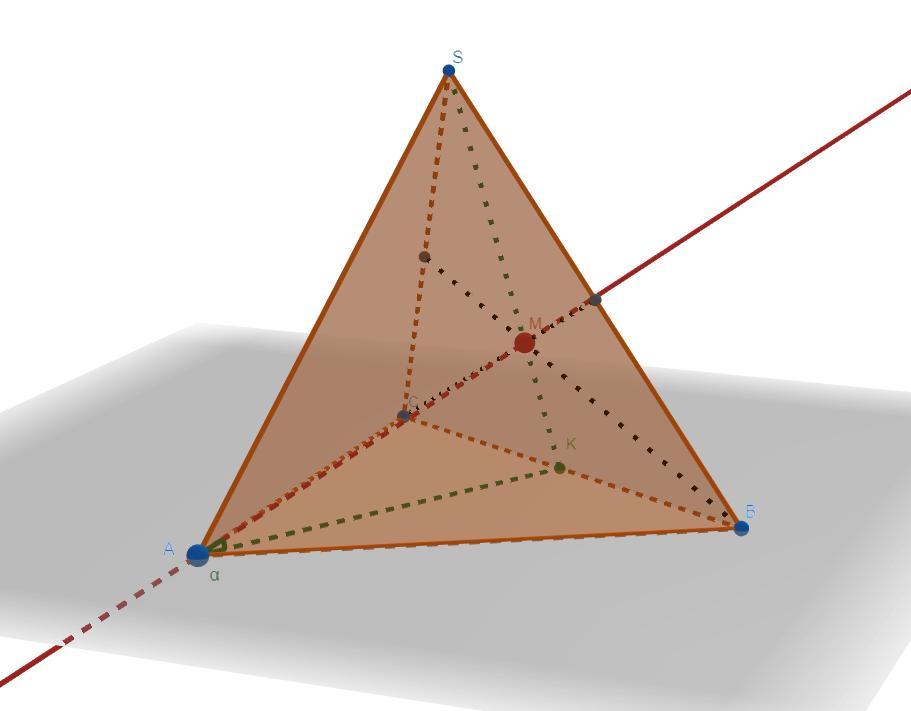
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад