Question

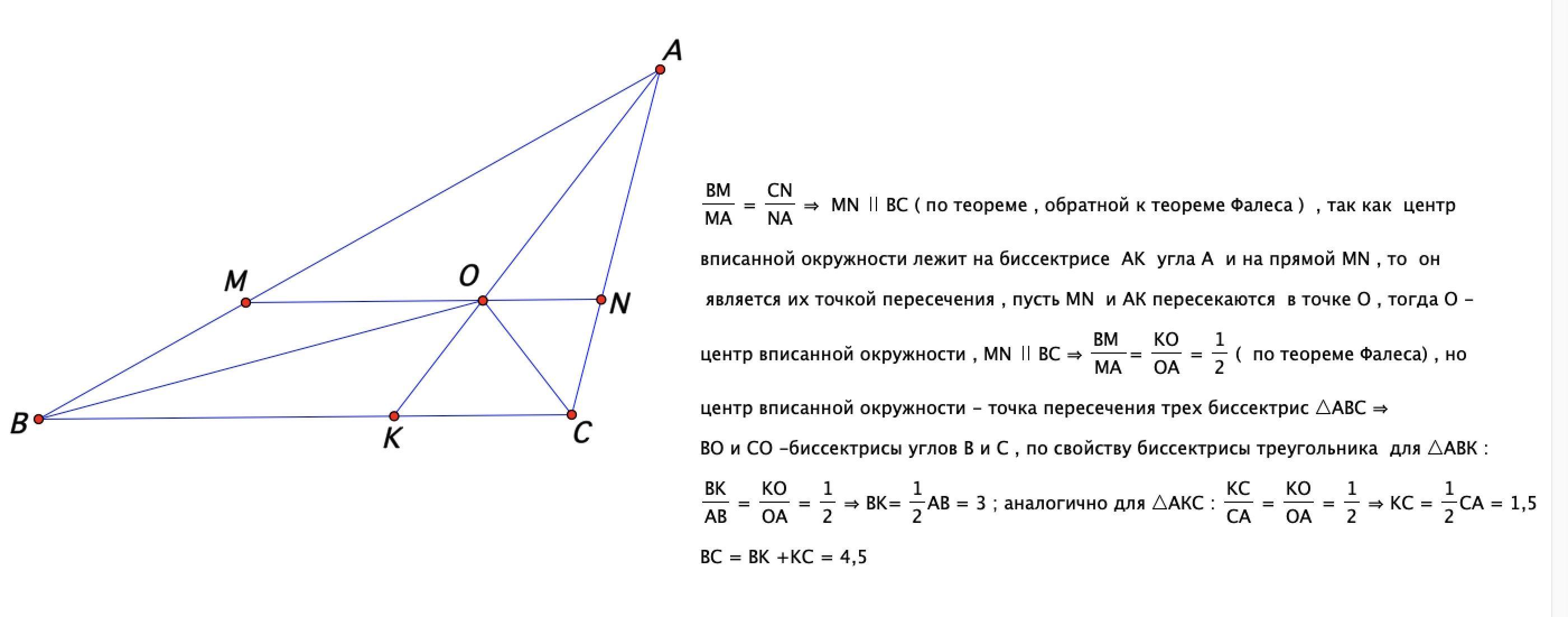
В треугольнике АBC на сторонах АВ и АС выбраны точки М и N так, что ВМ:МА=СN:NA=1:2. Оказалось , что отрезок МN содержит центр окружности , вписанной в треугольник АВС. Найдите ВС , если АВ=6 АС=3.

Answer 1

Будем пользоваться теоремой о биссектрисе.

Она заключается в следующем: отношение сторон треугольника, содержащихся в угле, из которого проведена биссектриса, равна отношению отрезков, на которые делит биссектриса противолежащую сторону.

Назовем точку пересечения MN и биссектрисы AK через R; Тогда из данного в условии легко вывести, что биссектриса угла C проходит через R. Пусть RC ∩ AB = F; Пусть AM=2x, MB=x. Тогда x=2; По теореме Менелая для треугольника AMN: $frac{AF}{FM}frac{MR}{RN}frac{NC}{AC}=1 Rightarrow frac{AF}{FM} =frac{1}{2timesfrac{1}{3} } =frac{3}{2}$, ну а отсюда легко получить AF=2,4 и FM=1,6; Значит BF=3,6 и AF=2,4; По вышеизложенной теореме о биссектрисе имеем: $frac{BC}{AC}= frac{BF}{AF}Leftrightarrow BC=frac{ACtimes BF}{AF}=frac{3times 3,6}{2,4}=4,5$

Answer 2

Ответ:

4,5

Объяснение: