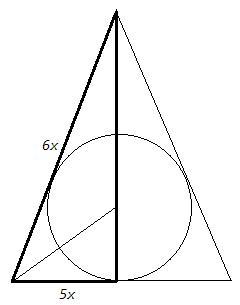
Найдите боковую сторону равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию в отношении 6 : 5 , считая от вершины, а основание равно 72 см.
Ответы
Ответ дал:
0
Центр вписанной окружности - точка пересечения биссектрис. Высота к основанию равнобедренного треугольника является биссектрисой и медианой. Биссектриса делит сторону треугольника в отношении прилежащих сторон. Следовательно боковая сторона (a) и половина основания (36) относятся как 6:5.
a/36 =6/5 <=> a =43,2 (см)
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад