Найдите угловой коэффициент касательной проведенной к графику функции
y=5x^3+2x-5 в его точке с абциссой x=3
Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
Приложения:
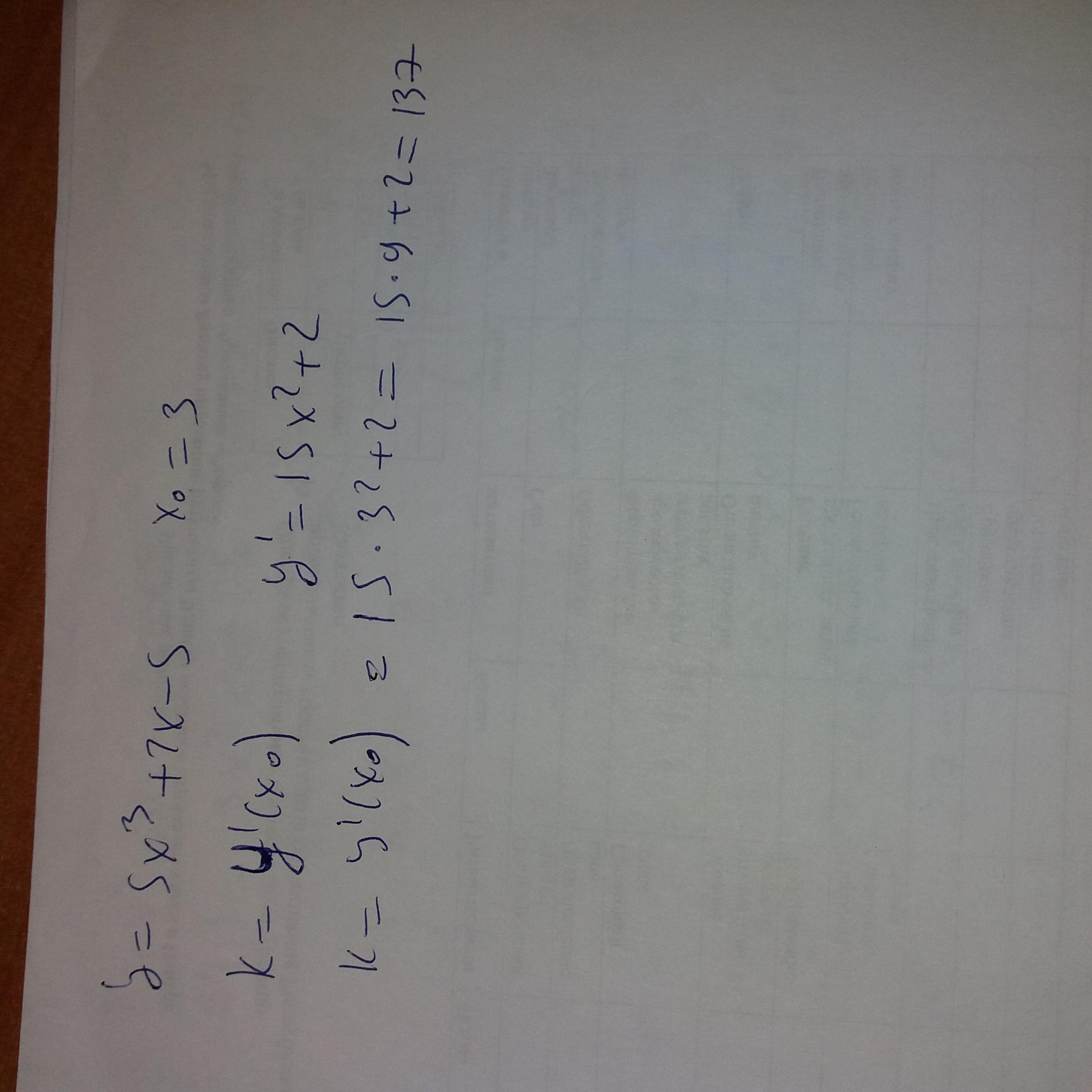
Ответ дал:
0
Ответ:
53
Пошаговое объяснение:
Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке. То есть:
f'(x_0)=k
Вычислим производную функции первого порядка:
y'=(5x^3-7x)'=15x^2-7
Тогда:
k=y'(2)=15cdot 2^2-7=53
Приложения:
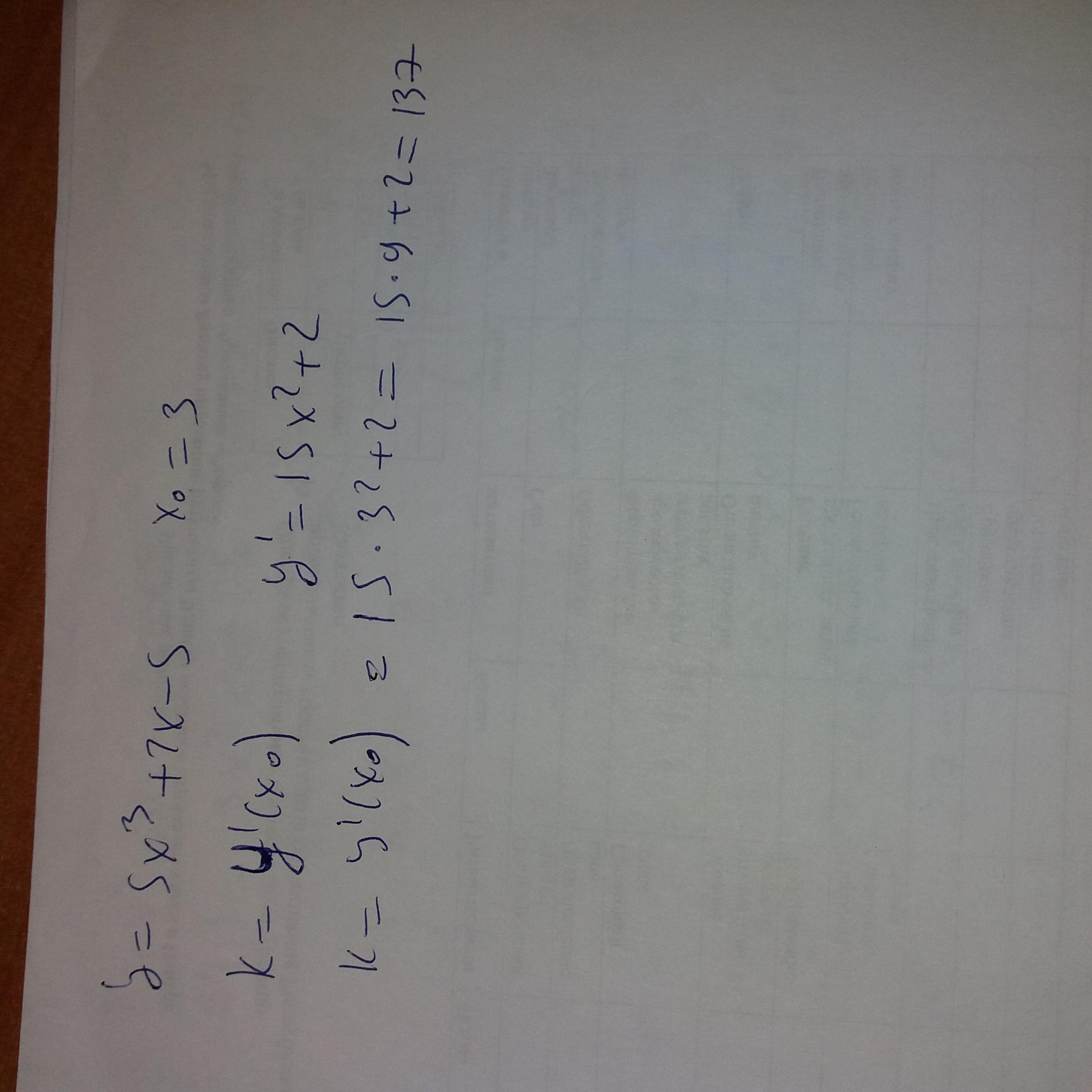
Ответ дал:
0
Отметь мой ответ лучшим PLEASE
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад