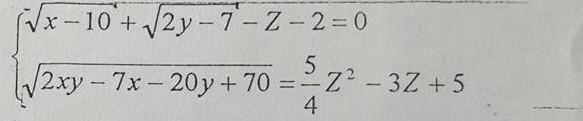Ответы
Ответ:
Объяснение:
Огонь
Ответ: z=2 ; x=14 ;y=5.5
Объяснение:
Преобразуем вторую часть уравнения под радикалом:
2xy-7x-20y+70=x*(2y-7) -10*(2y-7)=(x-10)*(2y-7)
Найдем дискриминант квадратного уравнения относительно z:
5/4 *z^2 -3z+5=0 (a>0- ветви параболы идут вверх)
5z^2-12z+20=0
D/4=6^2-5*20<0
Вывод: тк a>0 и D<0 ,то парабола положительна при любом z.
ОДЗ:
x>=10
y>=7/2
z+2>=0 ; z>=-2 (тк сумма радикалов неотрицательна).
Делаем замены:
√x-10 =a>=0
√2y-7=b>=0
a+b=z+2 → (a+b)^2=(z+2)^2 → 1) a^2+2ab+b^2=z^2+4z+4
ab=5/4 *z^2-3z+5
2 ) 4ab=5z^2-12z+20
Вычтем из уравнения 1 уравнение 2:
a^2-2ab+b^2=-4z^2+16z-16
(a-b)^2=- (4z^2-16z+16)
(a-b)^2=-(2z-4)^2
Очевидно,что тк (2z-4)^2>=0 ,то -(2z-4)^2<=0.
Но тк (a-b)^2>=0 , то и -(2z-4)^2>=0
Из этих двух условий выходит что:
2z-4=a-b=0
z=2 (удовлетворяет ОДЗ)
a=b
из уравнения: a+b=z+2
2a=4
a=b=2>0 (удовлетворяет ОДЗ)
Вернемся к заменам:
√(x-10)=2
x-10=4
x=14 (удовлетворяет ОДЗ)
√(2y-7)=2
2y-7=4
y=11/2=5.5 (удовлетворяет ОДЗ)
Ответ: z=2 ; x=14 ;y=5.5